题目内容
如图所示,一根跨越一固定水平光滑细杆的轻绳,两端各系一个小球,球Q置于地面,球P被拉到与细杆同一水平的位置。在绳刚被拉直时,球P从静止状态向下摆动,当球P摆到竖直位置时,球Q刚要离开地面,则两球质量之比mQ : mP为: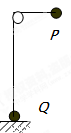
| A.4 | B.3 | C.2 | D.1 |
B
解析试题分析:球P从静止摆到最低位置的过程中,做圆周运动,绳的拉力始终与速度垂直不做功,仅有重力做功,机械能守恒,设球P摆到竖直位置时的速度为 ,根据机械能守恒定律得:
,根据机械能守恒定律得: ,解得:
,解得:
球P摆到竖直位置时受有竖直向上的拉力和竖直向下的重力,合力提供向心力,由牛顿第二定律得: ,解得:
,解得:
因当球P摆到竖直位置时,球Q刚要离开地面,则有: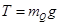 ,于是有:
,于是有: ,
,
所以两球质量之比mQ : mP为: ,故选B。
,故选B。
考点:本题考查了机械能守恒定律、牛顿第二定律、圆周运动等知识点,意在考查考生的理解能力、逻辑推理能力和综合应用能力。

 小学教材全测系列答案
小学教材全测系列答案如图所示,一质量为m的足球,以速度v由地面踢起,当它到达离地面高度为h的B点时(取地面为零势面,不计阻力),下列说法正确的是
A.在B点处的重力势能为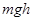 |
B.在B点处的机械能为 |
C.在B点处的动能为 |
D.在B点处的机械能为 |
在光滑的水平面上有三个完全相同的小球,它们成一条直线,2、3小球静止,并靠在一起,1小球以速度v0射向它们,如图所示.设碰撞中不损失机械能,则碰后三个小球的速度可能值是 
A.v1=v2=v3= v0 v0 | B.v1=0,v2=v3= v0 v0 |
C.v1=0,v2=v3= v0 v0 | D.v1=v2=0,v3=v0 |
内壁光滑的环形凹槽半径为R,固定在竖直平面内,一根长度为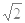 R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,小球乙位于凹槽的最低点(如图所示),由静止释放后
R的轻杆,一端固定有质量m的小球甲,另一端固定有质量为2m的小球乙.现将两小球放入凹槽内,小球乙位于凹槽的最低点(如图所示),由静止释放后 
| A.下滑过程中甲球的机械能变化量大小总是等于乙球的机械能变化量大小 |
| B.下滑过程中甲球减少的重力势能总是等于乙球增加的重力势能 |
| C.甲球可沿凹槽下滑到槽的最低点 |
| D.杆从右向左滑回时,乙球一定能回到凹槽的最低点 |
如图所示,固定曲面AC是一段半径为4.0米的光滑圆弧形成的,圆弧与水平方向相切于A点,AB=10cm,现将一小物体先后从圆弧顶端C和中点D处由静止释放,到达曲面低端时速度分别为v1和v2,所需时间为t1和t2,以下说法正确的是( )
| A.v1 > v2 , t1= t2 | B.v1 > v2 , t1 > t2 |
| C.v1 < v2 , t1= t2 | D.v1 < v2 , t1 > t2 |
(6分)如图所示,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为 的小球,B处固定质量为
的小球,B处固定质量为 的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直.放手后开始运动,在不计任何阻力的情况下,下列说法不正确的是( )
的小球,支架悬挂在O点,可绕过O点并与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直.放手后开始运动,在不计任何阻力的情况下,下列说法不正确的是( )
| A.A球到达最低点时速度为零 |
| B.A球机械能减少量等于B球机械能增加量 |
| C.B球向左摆动所能达到的最高位置应高于A球开始运动时的高度 |
| D.当支架从左向右回摆时,A球一定能回到起始高度 |
下列说法正确的是( )
| A.物体做匀速直线运动,机械能一定守恒 |
| B.物体所受的合力不做功,机械能一定守恒 |
| C.物体所受的合力不等于零,机械能可能守恒 |
| D.物体所受的合力等于零,机械能一定守恒 |
如图所示,从光滑的1/ 4圆弧槽的最高点滑下的小滑块,滑出槽口时速度方向为水平方向,槽口与一个半球顶点相切,半球底面为水平,若要使小物块滑出槽口后不沿半球面下滑,已知圆弧轨道的半径为R1,半球的半径为R2,则R1和R2应满足的关系是
| A.R1≤R2/2 |
| B.R1≥R2/2 |
| C.R1≤R2 |
| D.R1≥R2 |
 ,cos37°=
,cos37°=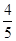 )
)