Question

【题目】某空间存在方向末知的匀强电场，一绝缘轻绳，一端固定在O点，另一端与一质量为m，电量为+q的带电小球相连，小球在竖直平面内恰好能做完于完整的圆周运动，在下列情况下，小球在最低点所受绳的拉力大小是多少。

（1）匀强电场方向竖直向上，大小为

（2）匀强电场方向竖直向下，大小为E2=

（3）匀强电场方向水平向右且与圆周运动轨迹所在平面平行，大小为E3=

Answer 1

【答案】（1）0（2）12mg（3）3（1+）mg

【解析】（1）加方向竖直向上匀强电场时，由于,而且小球在竖直平面内恰好能做完于完整的圆周运动，所以小球在最低点时速度最小为零，因而此时拉力最小；

（2）加方向竖直向下匀强电场时， ,小球在最高点，速度最小，有：

小球从A点到最低点，由动能定理有：

在最低点，有：

联产解得绳的拉力为： ；

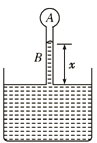
（2）加水平向右的匀强电场时,在等效最高点A点速度最小，如图所示：

且有： ，则： ，即：

在等效最高点A点，有：

小球从等效最高点A点到等效最低点B，由动能定理有：

在最低点，有： ，联立解得。