题目内容
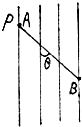
如图所示,长为l的绝缘细线一端悬于O点,另一端系一质量为m、电荷量为q的小球.现将此装置放在水平向右的匀强电场中,小球静止在A点,此时细线与竖直方向成37°角.重力加速度为g,sin37°=0.6,cos37°=0.8.
(1)判断小球的带电性质;
(2)求该匀强电场的电场强度E的大小;
(3)若将小球向左拉起至与O点处于同一水平高度且细绳刚好张紧,将小球由静止释放,求小球运动到最低点时的速度大小.

(1)判断小球的带电性质;
(2)求该匀强电场的电场强度E的大小;
(3)若将小球向左拉起至与O点处于同一水平高度且细绳刚好张紧,将小球由静止释放,求小球运动到最低点时的速度大小.

(1)由图可知,小球受到的电场力方向向左,电场方向向右,所以小球带负电.
(2)小球受三个力作用处于平衡状态,有tan37°=
可得:E=
.
(3)小球从水平位置到竖直方向的过程中重力和电场力做功,根据动能定理得mgL-qEL=
mv2
联立解得 v=
答:(1)小球带负电
(2)匀强电场电场强度的大小为
.
(3)小球经过A点时的速度为v=
(2)小球受三个力作用处于平衡状态,有tan37°=
| mg |
| qE |
| 4mg |
| 3q |
(3)小球从水平位置到竖直方向的过程中重力和电场力做功,根据动能定理得mgL-qEL=
| 1 |
| 2 |
联立解得 v=
|
答:(1)小球带负电
(2)匀强电场电场强度的大小为
| 4mg |
| 3q |
(3)小球经过A点时的速度为v=
|

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目