题目内容
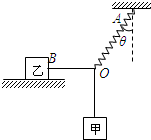如图所示，质量为m1=0.4Kg的物体甲通过二段轻绳和一个轻质细弹簧悬挂在结点O．轻绳OB水平且B端与放置在水平面上质量为m2=0.5Kg的物体乙相连，轻弹簧OA与竖直方向的夹角θ=370，物体甲、乙均处于静止状态．（已知：sin37°=0.6，cos37°=0.8，tan37°=0.75；g取10m/s2．）求：（1）若轻弹簧的劲度系数为K=500N/m，则轻弹簧的伸长长度是多大？
（2）物体乙受到的摩擦力是多大？方向如何？
（3）若物体乙的最大静摩擦力等于12N，则欲使物体乙在水平面上不滑动，物体甲的质量m1最大不能超过多少？（将AO替换为细绳，保持O点位置不变）
分析：（1）对物体受力分析，由几何关系可求得弹簧的拉力，再由胡克定律可求得弹簧伸长的长度；
（2）乙物体受OB的拉力及摩擦力而处于平衡，由几何关系求得拉力即可求得摩擦力；
（3）已知最大静摩擦力，由平衡关系可求得OB的拉力大小，由几何关系可求得甲物体的质量．
（2）乙物体受OB的拉力及摩擦力而处于平衡，由几何关系求得拉力即可求得摩擦力；
（3）已知最大静摩擦力，由平衡关系可求得OB的拉力大小，由几何关系可求得甲物体的质量．
解答：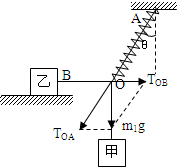
解：（1）对物体受力分析，如图所示：
由几何关系可知：弹簧的拉力T0A=
=
m1g=5N
由胡克定律可知：X=
=0.01m
（2）由图可知：OB的拉力TOB=m1gtanθ=
m1g=3N，而乙在水平方向受力平衡
所以乙受到的摩擦力f=TOB=3N
方向水平向左
（3）由题意及（2）的解答可知：
TOB=
m1g=fm=12N
解得甲的质量：
m1=1.6kg，即物体甲的质量m1最大不能超过1.6kg
答：（1）轻弹簧的伸长长度是0.01m；
（2）摩擦力为3N，方向水平向左；
（3）甲的质量不能超过1.6kg．
解：（1）对物体受力分析，如图所示：由几何关系可知：弹簧的拉力T0A=
| m1g |
| cosθ |
| 5 |
| 4 |
由胡克定律可知：X=
| TOA |
| K |
（2）由图可知：OB的拉力TOB=m1gtanθ=
| 3 |
| 4 |
所以乙受到的摩擦力f=TOB=3N
方向水平向左
（3）由题意及（2）的解答可知：
TOB=
| 3 |
| 4 |
解得甲的质量：
m1=1.6kg，即物体甲的质量m1最大不能超过1.6kg
答：（1）轻弹簧的伸长长度是0.01m；
（2）摩擦力为3N，方向水平向左；
（3）甲的质量不能超过1.6kg．
点评：本题中应先以结点O为研究对象得出几何关系，再对乙分析可得出摩擦力与OB拉力的关系；注意应共点力平衡问题一定要注意做出力的平行四边形，由几何关系求力．
练习册系列答案
相关题目
如图所示，质量为m1的物体甲通过三段轻绳悬挂，三段轻绳的结点为O．轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连，轻绳OA与竖直方向的夹角θ=37°，物体甲、乙均处于静止状态．（已知：sin37°=0.6，cos37°=0.8）求：
如图所示，质量为m1=10g的子弹以800m/s的速度向右射向放在光滑地面上静止的质量为2kg的物块．
如图所示，质量为m1=2.0kg、长为L=10.0m的平板小车，静止在光滑水平地面上，一质量为m2=0.5kg的小物块以v0=10.0m/s速度从左端冲上平板车，已知小物块与平板车之间的动摩擦因数μ=0.30．有关平板车和小物块最后的速度v'1和v'2的大小，以及整个过程中系统内能的增加量Q的计算试，正确的是（g=10m/s2）（ ）A、v′1=v′2=
| ||||||
B、v′1=v′2=
| ||||||
C、v′1＜
| ||||||
D、v′1＜
|
（2011?河南模拟）如图所示，质量为m1的木块受到水平向右的恒力F的作用沿质量为m2的长木板水平向右滑行，长木板保持静止状态．已知木块与长木板间的动摩擦因数为μ1，长木板与水平地面间的动摩擦因数为μ2，则（ ）
（2009?崇文区一模）如图所示，质量为m1=1kg的小物块P置于桌面上的A点并与弹簧的右端接触（不拴接），轻弹簧左端固定，且处于原长状态．质量M=3.5kg、长L=1.2m的小车静置于光滑水平面上，其上表面与水平桌面相平，且紧靠桌子右端．小车左端放有一质量m2=0.5kg的小滑块Q．现用水平向左的推力将P缓慢推至B点（弹簧仍在弹性限度内）时，撤去推力，此后P沿桌面滑到桌子边缘C时速度为2m/s，并与小车左端的滑块Q相碰，最后Q停在小车的右端，物块P停在小车上距左端0.5m处．已知AB间距离L1=5cm，AC间距离L2=90cm，P与桌面间动摩擦因数μ1=0.4，P、Q与小车表面间的动摩擦因数μ2=0.1，（g取10m/s2），求：