题目内容
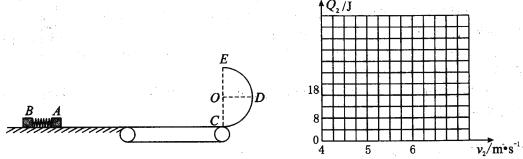
【题目】如图所示,足够长的光滑水平桌面与长度L=5.4m 的水平传送带平滑连接,传送带右端与半径r= 0.5m的光滑半圆轨道相切,半圆的直径CE竖直。A、B两小物块的质量分别为mA=4kg、mB=2kg,物块之间压缩着一根轻弹簧并用细绳锁定。当A、B在桌面上向右运动的速度υ1=1m/s时,细线断裂,弹簧脱离两物块后,A继续向右运动,并在静止的传送带上滑行了s=1.8m。已知物块与传送带间的动摩擦因数μ=0.25,重力加速度g = 10m/s2。求
(1)细线断裂后,弹簧释放的弹性势能EP ;
(2)若在物块A滑上传送带时,传送带立即以速度υ1=1m/s逆时针匀速运动,求物块与传送带之间因摩擦产生的热量Q1;
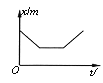
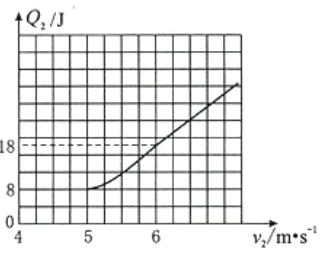
(3)若物块A滑仁传送带时,传送带立即以速度υ2顺时针匀速运动,为使A能冲上圆轨道,并通过最高点E,求υ2的取值范围,并作出物块与传送带之间因摩擦产生的热量Q2与υ2的关系图。(作图不需要推导过程,标示出关键点的横、纵坐标)
【答案】(1) Ep=24J(2) Q1= 32J (3) v2≥5m/s
【解析】
(1)设A、B与弹簧分离时的速度分别为vA、vB,以向右为正方向,由动量守恒定律
(mA+mB)v=mAvA+mBvB
A在桌面上运动,由动能定理
-μmAgs=0-![]()
联立解得
vA=3m/s
vB=-3m/s
弹簧释放的弹性势能为
Ep=![]() +
+![]() -
-![]()
解得Ep=24J ;
(2)A在传送带上向右减速,速度减为零后又向左加速,直到与传送带共速,之后向左离开传送带。设相对运动的时间为M加速度大小为
a=μg=2.5m/s2
由运动学公式
-v1=vA-at1
A的位移
![]()
传送带的位移
x带1=(-v1)·t1
滑块与传送带问的相对运动的路程为s1=x1-x带1
解得
摩擦生热Q1=μmAgs1=32J
(3)若传送带速度足够大,A将一直加速,此时A冲上圆轨道的速度最大。由运动学公式
![]()
解得vmax=6m/s
当A刚好能到达E点时,A冲上圆轨道的速度最小。在E点,由牛顿第二定律
mg=m![]()
A由C运动到E,由机械能守恒定律
mg·2r=![]()
联立解得vmin=5m/s
综上,v2≥5m/s
摩擦生热Q2与v2的关系如图
(i)当5m/s≤v2<6m/s时,A在传送带上先加速后匀速运动。A加速的位移
x2=![]()
A加速的时间t2=![]()
传送带的位移x带2=v2t2=![]()
A传送带的相对运动的路程
s2=x带2-x2=![]()
解得 Q2=μmAgs2=2![]() J
J
(ii)当v2>6m/s时,A在传送带上将一直加速。
A加速的位移![]() =L=5.4m
=L=5.4m
A加速度的时间![]() =
=![]() =1.2s
=1.2s
传送带的位移x带2′=v2t2′=1.2v2
A和传送带的相对运动的路程
s2′=x带2′-![]() =(1.2v2-5.4)m
=(1.2v2-5.4)m
解得Q2′=μmAgs2′=(12v2-54)J
综上,Q2=2![]() J(5m/s≤v2<6m/s),(12v2-54)J(v2≥6m/s)。
J(5m/s≤v2<6m/s),(12v2-54)J(v2≥6m/s)。

 名校课堂系列答案
名校课堂系列答案