Question

【题目】如图所示，在倾角为30°足够长的光滑斜面上有一长为l＝100 cm、开口向上的薄壁玻璃管，用长为l1＝50 cm的水银柱封闭一段空气柱。当玻璃管保持静止时，空气柱长为l2＝12.5 cm。已知玻璃管的横截面积S＝1 cm2，大气压强p0＝75 cmHg，水银的密度ρ＝13.6×103 kg/m3，玻璃管的质量与水银柱的质量相等，g取10 m/s2。

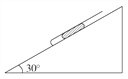
①若将玻璃管开口向下放置于斜面，且仍使其保持静止状态，求管内空气柱长度；

②在①问情形下，用沿斜面向上的恒力F拉玻璃管使其向上做匀加速直线运动，为了使水银柱不从管口溢出，求F的大小应满足的条件。

Answer 1

【答案】(1) 25 cm (2) 6.8 N<F≤13.6 N

【解析】①以管内气体为研究对象，管开口向上放置时气体压强：p1＝p0＋l1sin30°＝100cmHg

管开口向下放置时气体压强：p2＝p0－l1sin30°＝50cmHg

设空气柱长为l3，此过程气体发生等温变化，由玻意耳定律得p1V1＝p2V2

即p1l2S＝p2l3S，

代入数据解得l3＝25cm

②设管内水银柱的质量为m，则m＝ρl1S＝0.68kg

玻璃管整体能向上加速，则F>2mgsin30°＝6.8N

当水银柱下端到玻璃管口时，整体加速度最大，F也最大，此时，管内空气柱的长度为l4＝50cm。

设管内气压为p3，由玻意耳定律得：p2V2＝p3V3

代入数据解得p3＝25 cmHg

取水银柱为研究对象，由牛顿第二定律得：p0S－p3S－mgsin30°＝ma

取玻璃管和水银柱整体为研究对象，由牛顿第二定律得：F－2mgsin30°＝2ma

联立以上式子解得：F＝2(p0－p3)S＝13.6 N

综合以上得：6.8 N<F≤13.6 N。