题目内容
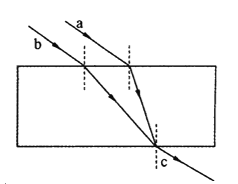
【题目】倾角为θ的斜面固定在水平面上,在斜面上放置一长木板,木板与斜面之间的动摩擦因数为μ。平行于斜面的力传感器上端连接木板,下端连接一光滑小球,如图所示。当木板固定时,传感器的示数为F1。现由静止释放木板,木板沿斜面下滑的过程中,传感器的示数为F2。则下列说法正确的是

A. 若μ=0,则F1=F2
B. 若μ=0,则F2=0
C. 若μ≠0,则μ=tanθ
D. 若μ≠0,则![]()
【答案】BD
【解析】
AB.当木板固定时,对小球分析,根据共点力平衡有:F1=mgsinθ,静止释放木板,木板沿斜面下滑的过程中,若μ=0,则整体沿斜面下滑时根据牛顿第二定律可得:Mgsinθ=Ma,解得:a=gsinθ,再以小球为研究对象,则有:mgsinθ-F2=ma,解得:F2=0,故A错误、B正确;
CD.当木板沿斜面下滑时,若μ≠0,对整体分析,根据牛顿第二定律可得加速度为:a=gsinθ-μgcosθ,隔离对小球分析有:mgsinθ-F2=ma,解得:F2=μmgcosθ,则有:![]() ,解得:
,解得:![]() ;故C错误、D正确.
;故C错误、D正确.

练习册系列答案
相关题目