题目内容
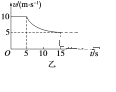
【题目】如图所示，竖直平面内固定一半径为R的光滑半圆环，圆心在O点。质量均为m的A、B两小球套在圆环上，用不可形变的轻杆连接，开始时球A与圆心O等高，球B在圆心O的正下方。轻杆对小球的作用力沿杆方向。
（1）对球B施加水平向左的力F，使A、B两小球静止在图示位置，求力的大小F；
（2）由图示位置静止释放A、B两小球，求此后运动过程中A球的最大速度v；
（3）由图示位置静止释放A、B两小球，求释放瞬间B球的加速度大小a。
【答案】（1）mg；（2）
；（3）
【解析】
（1）设圆环对
球的弹力为
，轻杆对球的弹力为
，对、
和轻杆整体，根据平衡条件有
对球有
解得
（2）当轻杆运动至水平时，、球速度最大且均为
，由机械能守恒有
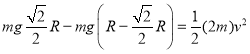
解得
（3）在初始位置释放瞬间，、速度为零，加速度都沿圆环切线方向，大小均为
，
设此时杆的弹力，根据牛顿第二定律
对球有
对球有
解得
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
