题目内容
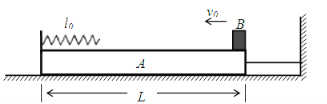
【题目】（18分）如图甲所示，放在光滑水平地面上的长木板质量M=0 5kg，木板右端放一质量m=0 5kg的滑块（可视为质点），滑块与木板间的动摩擦因数
=0 4；滑块的正上方有一悬点O，通过长l=0 8m的轻绳吊一质量m0=1 0kg的小球 现将小球拉至与O点处于同一水平位置，由静止释放，小球摆至最低点时与滑块发生正碰，且m0与m只碰一次，小球碰后的动能与其向上摆动高度的关系如图乙所示，g取10m/s2，求：
（1）碰前瞬间绳子对小球拉力的大小；
（2）碰后瞬间滑块速度的大小；
（3）要使滑块不会从木板上滑下，则木板的长度应滿足什么条件？
【答案】（1）30N （2）
（3）1m
【解析】
试题分析：（1）设小球摆动到最低点速度为
，绳对小球拉力为T，由机械能守恒定律得：
2分
解得：
1分
由牛顿第二定律得：
2分
解得：
1分
（2）设碰后小球、滑块速度分别为
和
，
由图像可得：
得：
，或
2分
小球与滑块碰撞过程动量守恒，得：
2分
解得：，或
计算碰撞前后的总动能可知：
，合理 1分
而 
，不合理 1分
所以碰后滑块速度只能取 1分
（3）当滑块和长木板共速时滑块恰好在木板的最右端，设板长为
由动量守恒得：
2分
由功能原理得：
2分
解得：l=1m 1分
练习册系列答案
灵星计算小达人系列答案
相关题目
