题目内容
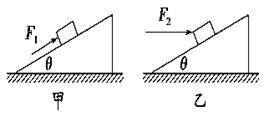
(10分)如图所示,物体的质量为2 kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=60°的拉力F,若要使两绳都能伸直,求拉力F的大小范围.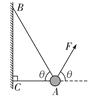
20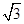 /3 N≤F≤40
/3 N≤F≤40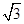 /3 N
/3 N
解析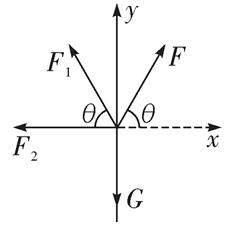
试题分析:物体A的受力如图所示,由平衡条件有
Fsin θ+F1sin θ-mg=0 ①
Fcos θ-F2-F1cos θ=0 ②
由①②式得F=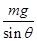 -F1 ③
-F1 ③
F=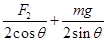 ④
④
要使两绳都能伸直,则有F1≥0 ⑤
F2≥0 ⑥
由③⑤式得F的最大值Fmax=mg/sin θ=40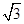 /3 N
/3 N
由④⑥式得F的最小值Fmin=mg/2sin θ=20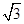 /3 N
/3 N
综合得F的取值范围为20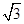 /3 N≤F≤40
/3 N≤F≤40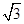 /3 N
/3 N
此题根据绳伸直且拉力分别为零的条件求出绳的拉力范围
考点:物体平衡

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为30°的斜面向上。绝缘斜面上固定有
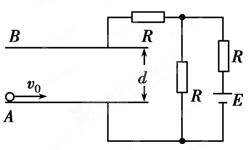
为30°的斜面向上。绝缘斜面上固定有 形状的光滑金属导轨MPN(电阻忽略不计),MP和NP长度均为2.5m,MN连线水平,长为3m。以MN中点O为原点、OP为x轴建立一维坐标系Ox。一根粗细均匀的金属杆CD,长度d为3m、质量m为1kg、电阻R为0.3Ω,在拉力F的作用下,从MN处以恒定的速度v=1m/s,在导轨上沿x轴正向运动(金属杆与导轨接触良好)。g取10m/s2。
形状的光滑金属导轨MPN(电阻忽略不计),MP和NP长度均为2.5m,MN连线水平,长为3m。以MN中点O为原点、OP为x轴建立一维坐标系Ox。一根粗细均匀的金属杆CD,长度d为3m、质量m为1kg、电阻R为0.3Ω,在拉力F的作用下,从MN处以恒定的速度v=1m/s,在导轨上沿x轴正向运动(金属杆与导轨接触良好)。g取10m/s2。
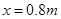 处电势差
处电势差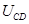 ;
;

 。
。
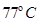 时,用一个软木塞封住瓶口,然后将烧杯中水温缓慢降至
时,用一个软木塞封住瓶口,然后将烧杯中水温缓慢降至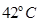 ,若想向上拔出软木塞,至少需要施加多大外力?已知大气压强
,若想向上拔出软木塞,至少需要施加多大外力?已知大气压强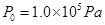 ,瓶口面积
,瓶口面积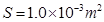 ,软木塞的重量
,软木塞的重量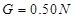 ,取热力学温度
,取热力学温度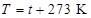 ,(软木塞与瓶口之间的摩擦不计).
,(软木塞与瓶口之间的摩擦不计).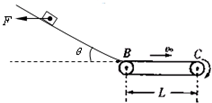
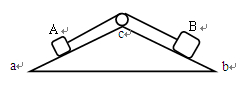
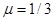 。现用平行于斜面的拉力F将木板B从木块A下面匀速抽出,同时C保持静止。(重力加速度g取10m/s2,sin370=0.6 cos370=0.8),求:
。现用平行于斜面的拉力F将木板B从木块A下面匀速抽出,同时C保持静止。(重力加速度g取10m/s2,sin370=0.6 cos370=0.8),求: