��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������ϵ�ĵ�һ�������д�ֱֽ���������ǿ�ų������������ӷֱ�����ͬ���ٶȴ�ԭ��O����ų�������ų����ٶȷ�����x��������н�Ϊ30�㡣��֪�������˶��Ĺ켣�뾶���ڸ����ӣ�������жϳ� ( )
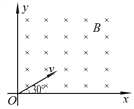
A. �����ӵıȺɴ��ڸ�����
B. �������ڴų����˶���ʱ����ڸ�����
C. �������ڴų����ܵ������������ڸ�����
D. �������뿪�ų�ʱ��λ�õ�ԭ��ľ�����ڸ�����
���𰸡�D
����������������������������˶��Ĺ켣�뾶���ڸ����ӣ�����Բ���˶��İ뾶�Ĺ�ʽ���Է����ó��ȺɵĴ�С��
���������˶������ڹ�ʽ���ڴų����˶��ĽǶȵĴ�С�����ж������˶���ʱ��Ĵ�С��
�⣺A���������ӵ��˶��İ뾶��ʽR=![]() �������������˶��Ĺ켣�뾶���ڸ����ӣ����������ӵıȺ�
�������������˶��Ĺ켣�뾶���ڸ����ӣ����������ӵıȺ�![]() С�ڸ����ӵıȺɣ�����A����
С�ڸ����ӵıȺɣ�����A����
B����������������ƫ����Y���������뿪�ų����ڴų����˶���![]() ����������t1=
����������t1=![]() T1
T1
��������������ƫ����X���������뿪�ų����ڴų����˶���![]() ����������t2=
����������t2=![]() T2
T2
�����ڹ�ʽT=![]() ��֪��������Ⱥ����ɷ��������ʣ�T1��T2
��֪��������Ⱥ����ɷ��������ʣ�T1��T2
���ԣ�t1��t2������B����
C�����������ڴų����˶����������������������ṩ�ģ�������������F=qvB��֪������q��С��ϵδ֪�����Բ��ܱȽ��������Ĵ�С������C����
D���������ڴų����˶���![]() �����������뿪�ų�ʱ�����꣺Y=
�����������뿪�ų�ʱ�����꣺Y=![]() r1
r1
�������ڴų����˶���![]() �����������뿪�ų�ʱ�����꣺X=r2
�����������뿪�ų�ʱ�����꣺X=r2
�����⣬r1��r2����Y��X������D��ȷ��
��ѡ��D��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�