题目内容
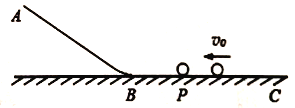
【题目】如图所示AB为足够长的光滑斜面轨道，通过一段光滑的圆弧与光滑水平轨道BC相连，质量为m的小球P静止在水平轨道上，用不同质量的小球以速度v0分别与小球P发生弹性正碰，求球P在斜面上能达到的最大高度。
【答案】
【解析】
不同质量的小球以速度v0分别与小球P发生弹性正碰，根据动量守恒和能量守恒求出碰后P球的速度，进行分析知，当M
m时，v2有最大值，然后根据机械能守恒可得球P在斜面上能达到的最大高度。
设质量为M的小球与P球弹性正碰后速度变为v1，P球速度变为v2，由动量守恒和能量守恒有：
Mv0=Mv1+mv2
Mv02=Mv12+mv22
求解可得：v2=
v0=
当Mm时，v2有最大值2v0
设P球上升的最大高度为h，根据机械能守恒有：
mv22=mgh
球P在斜面上能达到的最大高度:h=
=
练习册系列答案
相关题目
