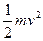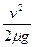题目内容
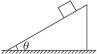
如下图所示，在北戴河旅游景点之一的南戴河滑沙场，有两个坡度不同的沙坡滑道AB和AC（都可以看作斜面），甲、乙两名旅游者分别乘坐两个滑沙撬从坡顶同一水平线上由静止滑下，最后都停在水平沙面CD上.设滑沙撬和沙面间的动摩擦因数μ处处相同，滑沙者保持一定姿势坐在沙撬上不动，请回答：
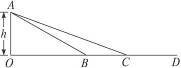
（1）他们滑到各自的坡底B点和C点时的速度是否相同？
（2）他们停下的位置距离坡顶的水平距离是否相同？
（1）他们滑到各自的坡底B点和C点时的速度是否相同？
（2）他们停下的位置距离坡顶的水平距离是否相同？
（1）他们滑到各自的坡底B点和C点时的速度不同；
（2）他们停下的位置距离坡顶的水平距离相同.
（2）他们停下的位置距离坡顶的水平距离相同.
（1）设他们滑到坡底时的速度为v，坡长为l，坡底长为s，
根据动能定理得：
mgh-μmglcosθ＝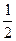
mv2
v=
因为两个坡底长s大小不同，所以雪橇在坡底B点和C点时的速度不同，B点的速度比C点的大.
（2）设他们在水平沙面上继续滑行的距离为s′，由动能定理得：
-μmgs′=0-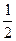mv2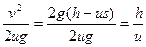，s′=
-s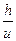
s′+s=
-s+s=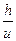，可见，停下的位置与坡长无关，故他们停下的位置距离坡顶的水平距离相同.
根据动能定理得：
mgh-μmglcosθ＝
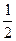mv2v=
因为两个坡底长s大小不同，所以雪橇在坡底B点和C点时的速度不同，B点的速度比C点的大.
（2）设他们在水平沙面上继续滑行的距离为s′，由动能定理得：
-μmgs′=0-
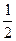mv2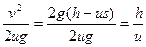，s′=-s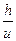s′+s=
-s+s=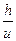，可见，停下的位置与坡长无关，故他们停下的位置距离坡顶的水平距离相同.
练习册系列答案
相关题目
量为m=1kg的物体与水平面间的动摩擦因数μ=0.6，在F=10N水平拉力作用下，由静止开始前进x1=2m后撤去外力， g=10m/s2,求：
轨道底端与水平地面相切。弹射装置将一个小球（可视为质点）从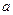
点水平弹射向 
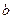点并进入轨道，经过轨道后从
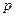点水平抛出，已知小物体与地面
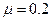，不计其它机械能损失，
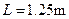，圆的半径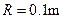
，小物体质量
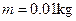，轨道质量为
，
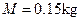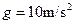，求：
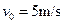，小物体从
至少为多大时，可出现轨道对地面的瞬时压力为零。
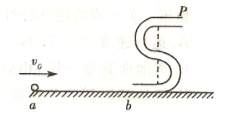
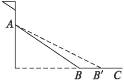
mv2
