��Ŀ����
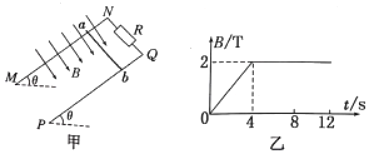
����Ŀ����ͼ��ʾ����ֱƽ���ڰ뾶R��045m�Ĺ⻬��Բ�ι��BCD�������Ϊ37����б����B�㴦Բ�����ӡ�A��D����ȸߣ���A���̶�һ������������m��0.2kg��С��飨�ɿ����ʵ㣩�ӵ������������ض�Ħ����������0.5��б���»�������B��ʱ�ٶ�Ϊ![]() m/s��Ȼ��ͨ����Բ�ι����D��ˮƽ�ɳ�����
m/s��Ȼ��ͨ����Բ�ι����D��ˮƽ�ɳ�����
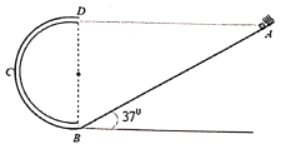
��1��С��鱻���������������У��������ͷŵĵ������ܣ�
��2��С�����D��ʱ�Թ������������
��3��С����D��ɳ�������б������B��ľ��롣
���𰸡���1��0.8J��2��0.2N���������£�3��0.75m
��������
��1��С���屻������B��Ĺ��̣��ɶ��ܶ�����
W��+��mgsin37������mgcos37����LAB��![]() ��0
��0
����LAB��![]()
��ã�W����0.8J
�ɹ��ܹ�ϵ�ã����ɵĵ�������EP��0.8J
��2����B��D�Ĺ����ɶ��ܶ����ã���mg2R��![]()
��ã�vD��2m/s
��D����ţ�ٵڶ����ɵã�FN+mg��m![]()
������ã�FN����0.2N
��ţ�ٵ�������֪�Թ���ڱڵ�������Ϊ0.2N����������
��3�����D�ɳ���б���ʱ��Ϊt����ƽ���˶��Ĺ��ɵ�
��ֱ����y��![]()
ˮƽ����x��vDt
�ɼ��ι�ϵ�ã�tan37����![]()
������ã�t��0.3s
�����б���ϵ�λ��ΪP����PB��![]()
��ã�PB��0.75m