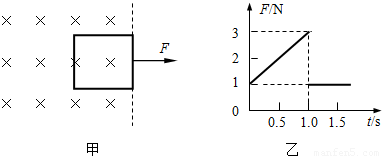题目内容
一正方形光滑金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲.t=0时刻对线框施加一水平向右的外力F,让线框从静止开始在水平面做匀加速直线运动穿过磁场.外力F随时间t变化的图线如图乙所示.已知线框质量m=1kg、电阻R=1Ω,求:
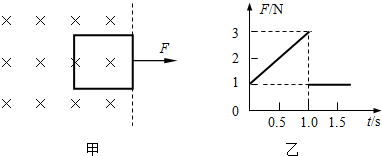
(1)匀强磁场的磁感应强度B;
(2)线框穿过磁场的过程中,通过线框的电荷量q.
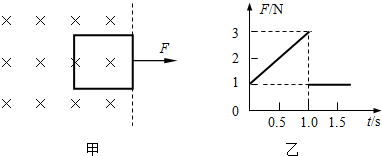
(1)匀强磁场的磁感应强度B;
(2)线框穿过磁场的过程中,通过线框的电荷量q.
分析:(1)当t=0时线框的速度为零,没有安培力,根据牛顿第二定律求出加速度a.由运动学公式求出线框刚出磁场时的速度,得到安培力表达式,由牛顿第二定律即可求出B;
(2)根据法拉第电磁感应定律、欧姆定律结合求出电量.
(2)根据法拉第电磁感应定律、欧姆定律结合求出电量.
解答:解:(1)t=0时刻,线框的速度为零,线框没有感应电流,不受安培力,加速度为a=
=
m/s2=1m/s2
线框的边长为 L=
at2=
×1×12m=0.5m
线框刚出磁场时的速度为 v=at=1×1m/s=1m/s,此时线框所受的安培力为FA=BIL,I=
,
则得 FA=
根据牛顿第二定律得 F-FA=ma
代入得 F-
=ma
代入数据 F=3N,m=1kg,R=1Ω,L=0.5m,v=1m/s,a=1m/s2解得,B=2
T
(2)由q=
△t,
=
,
=
,得
电量q=
=
=
C=
C
答:(1)匀强磁场的磁感应强度B是2
T;
(2)线框穿过磁场的过程中,通过线框的电荷量q是
C.
| F |
| m |
| 1 |
| 1 |
线框的边长为 L=
| 1 |
| 2 |
| 1 |
| 2 |
线框刚出磁场时的速度为 v=at=1×1m/s=1m/s,此时线框所受的安培力为FA=BIL,I=
| BLv |
| R |
则得 FA=
| B2L2v |
| R |
根据牛顿第二定律得 F-FA=ma
代入得 F-
| B2L2v |
| R |
代入数据 F=3N,m=1kg,R=1Ω,L=0.5m,v=1m/s,a=1m/s2解得,B=2
| 2 |
(2)由q=
. |
| I |
. |
| I |
| ||
| R |
. |
| E |
| △Φ |
| △t |
电量q=
| △Φ |
| R |
| BL2 |
| R |
2
| ||
| 1 |
| ||
| 2 |
答:(1)匀强磁场的磁感应强度B是2
| 2 |
(2)线框穿过磁场的过程中,通过线框的电荷量q是
| ||
| 2 |
点评:本题的突破口是根据牛顿第二定律求出加速度,再根据运动学公式求出线框的边长和速度,问题就变得简单清晰了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
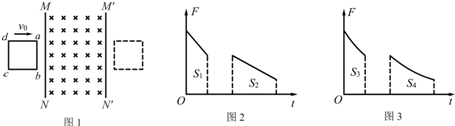
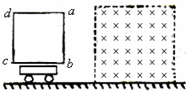 如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg.在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直.现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2.求:
如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg.在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直.现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2.求: