题目内容
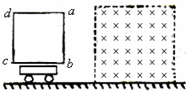 如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg.在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直.现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2.求:
如图所示,光滑水平面停放一小车,车上固定一边长为L=0.5m的正方形金属线框abcd,金属框的总电阻R=0.25Ω,小车与金属框的总质量m=0.5kg.在小车的右侧,有一宽度大于金属线框边长,具有理想边界的匀强磁场,磁感应强度B=1.0T,方向水平且与线框平面垂直.现给小车一水平速度使其向右运动并能穿过磁场,当车上线框的ab边刚进入磁场时,测得小车加速度a=10m/s2.求:(1)金属框刚进入磁场时,小车的速度为多大?
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为多少?
分析:(1)由题知道了线框的ab边刚进入磁场时小车的加速度,通过其受力情况,根据感应电动势、欧姆定律和牛顿第二定律结合求出速度.
(2)在求得金属框刚进入磁场时小车的速度后,为了求得从金属框刚要进入磁场,到其完全离开磁场所产生的焦耳热,关键在于求出小车完全离开磁场时的速度.根据动量定理和平均电流与磁通量变化的关系求出小车完全离开磁场时的速度,根据能量守恒定律求出热量.
(2)在求得金属框刚进入磁场时小车的速度后,为了求得从金属框刚要进入磁场,到其完全离开磁场所产生的焦耳热,关键在于求出小车完全离开磁场时的速度.根据动量定理和平均电流与磁通量变化的关系求出小车完全离开磁场时的速度,根据能量守恒定律求出热量.
解答:解:(1)设小车初速度为v0,则线框刚进入磁场时,ab边由于切割磁感线产生的电动势为:
E=BLv0…①
回路中的电流:I=
…②
根据牛顿定律:BIL=ma…③
由以上三式可解得:v0=5m/s
(2)设线框全部进入磁场时小车速度为v1,进入过程平均电流为
,所用时间为△t,则
=
=
…④
根据动量定理得
-B
L△t=mmv1-mv0…⑤
解得:v1=4m/s
设线框离开磁场时小车速度为v2,进入过程平均电流为
,所用时间为△t1,则:
=
=
…⑥
根据动量定理得
-B
L△t1=mv2-mv1…⑦
解得:v2=3m/s
线框从进入到离开产生的焦耳热应等于系统损失的机械能,即:
Q=
m
-
m
=4.0J
答:
(1)金属框刚进入磁场时,小车的速度为5m/s.
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为4.0J.
E=BLv0…①
回路中的电流:I=
| E |
| R |
根据牛顿定律:BIL=ma…③
由以上三式可解得:v0=5m/s
(2)设线框全部进入磁场时小车速度为v1,进入过程平均电流为
. |
| I |
. |
| I |
| △Φ |
| R△t |
| BL2 |
| R△t |
根据动量定理得
-B
. |
| I |
解得:v1=4m/s
设线框离开磁场时小车速度为v2,进入过程平均电流为
. |
| I1 |
. |
| I1 |
| △Φ |
| R△t1 |
| BL2 |
| R△t1 |
根据动量定理得
-B
. |
| I1 |
解得:v2=3m/s
线框从进入到离开产生的焦耳热应等于系统损失的机械能,即:
Q=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 2 |
答:
(1)金属框刚进入磁场时,小车的速度为5m/s.
(2)从金属框刚要进入磁场开始,到其完全离开磁场,线框中产生的焦耳热为4.0J.
点评:本题第1问是常规题,安培力经验公式F安=
要会推导.第2问运用动量定理研究非匀变速运动的速度要学会运用.
| B2L2v |
| R |

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求:
如图所示,光滑水平面AB与竖直面内的半圆形导轨在B点相接,导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放,在弹力作用下物体获得某一向右速度后脱离弹簧,脱离弹簧后当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍,之后向上运动完成半个圆周运动恰好到达C点.试求: 如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
如图所示,光滑水平面与一半径为R处在竖平面内的光滑圆轨道相切,质量为m的小球(可视为质点)以初速度v0向右运动进入圆轨道,在图中虚线位置脱离轨道,重力加速度为g,下述说法正确的是( )
 (2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求:
(2013?如东县模拟)如图所示,光滑水平面AB与竖直面内粗糙的半圆形导轨在B点衔接,BC为导轨的直径,与水平面垂直,导轨半径为R,一个质量为m的小球将弹簧压缩至A处.小球从A处由静止释放被弹开后,以速度v经过B点进入半圆形轨道,之后向上运动恰能沿轨道运动到C点,求: 如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )
如图所示,光滑水平面内,一根细绳一端固定,另一端系一小球,现让小球在水平面内做匀速圆周运动,则( )