题目内容
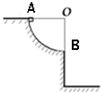
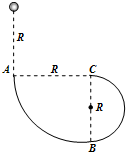
如图所示,质量为m的小球自由下落高度为R后沿竖直平面内的轨道ABC运动.AB是半径为R的1/4粗糙圆弧,BC是直径为R的光滑半圆弧,小球运动到C时对轨道的压力恰为零.B是轨道最低点.求:
(1)小球在AB弧上运动时,摩擦力对小球做的功.
(2)小球经B点前、后瞬间对轨道的压力之比.
(3)小球离开C点后竖直下落多少高度才能撞上圆轨道?
(1)小球在AB弧上运动时,摩擦力对小球做的功.
(2)小球经B点前、后瞬间对轨道的压力之比.
(3)小球离开C点后竖直下落多少高度才能撞上圆轨道?

(1)小球在C点:根据牛顿第二定律得
mg=m
小球由静止释放到C点过程,据动能定理得
mgR+Wf=
mvC2
联立解得Wf=-
mgR
(2)小球由静止释放到B点过程,据动能定理得
2mgR+Wf=
mvB2
在B点前瞬间据牛顿第二定律得
FN前-mg=m
在B点后瞬间据牛顿第二定律得
FN后-mg=m
由牛顿第三定律知,小球对轨道的压力大小等于轨道对小球的支持力大小.
联立解得 FN前:F N后=7:12
(3)小球离开C点后做平抛运动,合位移等于半径,根据平抛运动的分位移公式,有:
x=vct
y=
gt2
R2=x2+y2
联列解得:y=
R≈0.618R
答:(1)小球在AB弧上运动时,摩擦力对小球做的功为-
mgR.
(2)小球经B点前、后瞬间对轨道的压力之比为7:12.
(3)小球离开C点后竖直下落0.618R的高度才能撞上圆轨道.
mg=m
| ||
|
小球由静止释放到C点过程,据动能定理得
mgR+Wf=
| 1 |
| 2 |
联立解得Wf=-
| 3 |
| 4 |
(2)小球由静止释放到B点过程,据动能定理得
2mgR+Wf=
| 1 |
| 2 |
在B点前瞬间据牛顿第二定律得
FN前-mg=m
| ||
| R |
在B点后瞬间据牛顿第二定律得
FN后-mg=m
| ||
|
由牛顿第三定律知,小球对轨道的压力大小等于轨道对小球的支持力大小.
联立解得 FN前:F N后=7:12
(3)小球离开C点后做平抛运动,合位移等于半径,根据平抛运动的分位移公式,有:
x=vct
y=
| 1 |
| 2 |
R2=x2+y2
联列解得:y=
| ||
| 2 |
答:(1)小球在AB弧上运动时,摩擦力对小球做的功为-
| 3 |
| 4 |
(2)小球经B点前、后瞬间对轨道的压力之比为7:12.
(3)小球离开C点后竖直下落0.618R的高度才能撞上圆轨道.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目