题目内容
如图所示,物体A、B通过定滑轮以细绳相连,已知两物体的质量mA>mB,使两物体A、B位于同一水平面,当它们离地面的高度为h时,由静止开始释放,若不计滑轮质量及一切阻力,求当A被释放后,物体B能上升的最大距离.
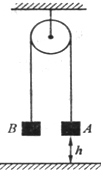

A下降,B上升的过程,以AB组成的系统为研究对象,由于只有重力做功,系统的机械能守恒,设A落地时的速度大小为v,根据系统机械能守恒定律得:
mAgh=mBgh+
(mA+mB)v2…①
A落地后,B上升的过程,设B继续上升的最大高度为h′,根据机械能守恒得:
mAgh′=
mAv2②
由①②得:h′=
h
故物体B能上升的最大距离 H=h+h′=
h
答:物体B能上升的最大距离为
h.
mAgh=mBgh+
| 1 |
| 2 |
A落地后,B上升的过程,设B继续上升的最大高度为h′,根据机械能守恒得:
mAgh′=
| 1 |
| 2 |
由①②得:h′=
| mA-mB |
| mA+mB |
故物体B能上升的最大距离 H=h+h′=
| 2mA |
| mA+mB |
答:物体B能上升的最大距离为
| 2mA |
| mA+mB |

练习册系列答案
相关题目