题目内容
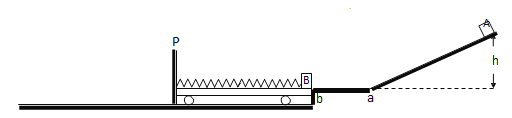
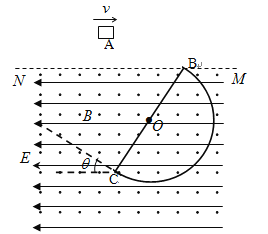
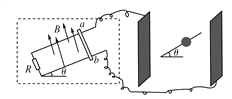
【题目】如图所示在虚线空间内有一对彼此平行的金属导轨，宽为L，与水平面的夹角为θ，导轨电阻不计，在虚线空间内同时分布着垂直导轨平面上的磁感应强度为B的匀强磁场．导轨的下端接一定值电阻R，上端通过导线与一对竖直放置的平行金属板相连接，两板间距为d，其间固定着一光滑绝缘直杆，它与水平面也成θ角，杆上套一带电小球．当一电阻也为R的光滑导体棒ab沿导轨以速度v匀速下滑时，小球恰好静止在绝缘直杆上．则由此可以判断小球的电性并能求出其荷质比为( )
A. 正电荷，2dgtanθ/BLvcosθ
B. 正电荷，2dgtanθ/BLv
C. 负电荷，2dgtanθ/BLvcosθ
D. 负电荷，2dgtanθ/BLv
【答案】B
【解析】杆切割磁感线产生的感应电动势：E=BLv，两金属板间的电压： 
，杆匀速下滑，由右手定则可知，杆的a端电势高，两金属板间的电场水平向右，小球受到竖直向下的重力，垂直于杆斜向左上方的支持力，小球要静止，受到的电场力应水平向右，小球受到的电场力方向与场强方向相同，小球带正电；两金属板间的电场强度：
，小球静止，处于平衡状态，由平衡条件得：qE=mgtanθ，解得小球的荷质比：
，故B正确，ACD错误。
练习册系列答案
相关题目
