题目内容
如图所示,在倾角为θ的斜面上,轻质弹簧一与斜面底端固定,另一端与质量为M的平板A连接,一个质量为m的物体B靠在平板的右测,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态,现放手,使A和B一起沿斜面向上运动距离L时,A和B达到最大速度v.则以下说法正确的是( )

| A.A和B达到最大速度v时,弹簧是自然长度 | ||
| B.若运动过程中A和B能够分离,则A和B恰好分离时,二者加速度大小均为g(sinθ+μcosθ) | ||
C.从释放到A和B达到最大速度v的过程中.弹簧对A所做的功等于
| ||
D.从释放到A和B达到最大速度v的过程中,B受到的合力对它做的功等于
|

A、A和B达到最大速度v时,A和B的加速度应该为零.
对AB整体:由平衡条件知
kx-(m+M)gsinθ-μ(m+M)gcosθ=0,
所以此时弹簧处于压缩状态.故A错误.
B、A和B恰好分离时,AB间的弹力为0,对B受力分析:由牛顿第二定律知,
沿斜面方向,mgsinθ+μmgcosθ=ma,
得a=gsinθ+μgcosθ,
由牛顿第二定律知,A,B的加速度相同,故B正确.
C、从释放到A和B达到最大速度v的过程中,对于AB整体,根据动能定理得
-(m+M)gLsinθ-μ(m+M)gcosθ?L+W弹=
(m+M)v2
弹簧对A所做的功W弹=
(m+M)v2+(m+M)gLsinθ+μ(m+M)gcosθ?L,故C错误.
D、从释放到A和B达到最大速度v的过程中,对于B,根据动能定理得
B受到的合力对它做的功W合=△Ek=
mv2,故D正确.
故选:BD.
对AB整体:由平衡条件知
kx-(m+M)gsinθ-μ(m+M)gcosθ=0,
所以此时弹簧处于压缩状态.故A错误.
B、A和B恰好分离时,AB间的弹力为0,对B受力分析:由牛顿第二定律知,
沿斜面方向,mgsinθ+μmgcosθ=ma,
得a=gsinθ+μgcosθ,
由牛顿第二定律知,A,B的加速度相同,故B正确.
C、从释放到A和B达到最大速度v的过程中,对于AB整体,根据动能定理得
-(m+M)gLsinθ-μ(m+M)gcosθ?L+W弹=
| 1 |
| 2 |
弹簧对A所做的功W弹=
| 1 |
| 2 |
D、从释放到A和B达到最大速度v的过程中,对于B,根据动能定理得
B受到的合力对它做的功W合=△Ek=
| 1 |
| 2 |
故选:BD.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
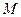 的滑块
的滑块 套在光滑的水平杆上可自由滑动,质量为
套在光滑的水平杆上可自由滑动,质量为 的小球
的小球 用一长为
用一长为 的轻杆与
的轻杆与 点相连接,轻杆处于水平位置,可绕
点相连接,轻杆处于水平位置,可绕
 ,不固定滑块且给小球一竖直向上的初速度
,不固定滑块且给小球一竖直向上的初速度 ,则当轻杆绕
,则当轻杆绕



