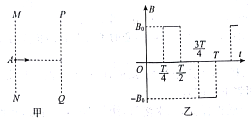
[题目]如图所示.在直角坐标系xoy的第一象限中有两个全等的直角三角形区域Ⅰ和Ⅱ.充满了方向均垂直纸面向里的匀强磁场.区域Ⅰ的磁感应强度大小为B0.区域Ⅱ的磁感应强度大小可调. C点坐标为(4L.3L).M点为OC的中点.质量为m带电量为-q的粒子从C点以平行于y轴方向射入磁场Ⅱ中.速度大小为 .不计粒子所受重力.粒子运动轨迹与磁场区域相切时认为粒子能再次进题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，在直角坐标系xoy的第一象限中有两个全等的直角三角形区域Ⅰ和Ⅱ，充满了方向均垂直纸面向里的匀强磁场，区域Ⅰ的磁感应强度大小为B0，区域Ⅱ的磁感应强度大小可调， C点坐标为（4L，3L），M点为OC的中点。质量为m带电量为-q的粒子从C点以平行于y轴方向射入磁场Ⅱ中，速度大小为，不计粒子所受重力，粒子运动轨迹与磁场区域相切时认为粒子能再次进入磁场。

（1）若粒子无法进入区域Ⅰ中，求区域Ⅱ磁感应强度大小范围；

（2）若粒子恰好不能从AC边射出，求区域Ⅱ磁感应强度大小；

【答案】（1）（2）

【解析】试题分析：平面几何做图，可知粒子在磁场中的轨迹与OD边相切，可求其半径，由粒子在磁场中的运动规律可求，磁感应强度大小范围；若粒子恰好不能从AC边射出，则粒子在磁场中与AC边相切，由几何关系，求粒子在磁场Ⅱ中的半径，由粒子在磁场中的运动规律可求解区域Ⅱ磁感应强度大小。

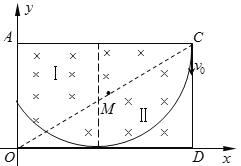
（1）如图所示，当运动轨迹与x轴相切时，粒子恰好无法进入区域Ⅰ中。由几何关系可知粒子圆周运动半径为，

由得

若粒子无法进入区域Ⅰ中，求区域Ⅱ磁感应强度

（2）若粒子恰好不能从AC边射出，粒子轨迹与AC边相切于E点，由几何关系可知

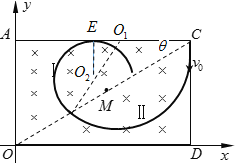
粒子在磁场Ⅰ中，

可得粒子在磁场Ⅰ中半径为

设在磁场Ⅱ中的半径为R，由几何关系可知，

由于可知

解得

在磁场Ⅱ中由，

可知

练习册系列答案

（1）A、B相碰后的瞬间，整体共同速度v的大小；

（2）A、B相碰后，整体以a=5m/s2的加速度向下加速运动时，地面对物块C的支持力FN；

（3）若要A、B碰后物块C能够离开地面，物块A由静止释放位置距物块B的高度最小值h多大。

【题目】某同学把电流表、干电池和一个定值电阻串联后，两端连接两支测量表笔，做成了一个测量电阻的装置，如图所示。两支表笔直接接触时，电流表的读数为满偏电流Ig；两支表笔与400的电阻相连时，电流表的读数为Ig /3 。以下说法正确的是：

A. 该测量电阻装置的内阻200，图中A接黑表笔

B. 该测量电阻装置的内阻200，图中A接红表笔

C. 该测量电阻装置的内阻400，图中A接黑表笔

D. 该测量电阻装置的内阻400，图中A接红表笔

【题目】如图所示，长为L的轻质硬杆A一端固定小球B，另一端固定在水平转轴O上。现使轻杆A绕转轴O在竖直平面内匀速转动，轻杆A与竖直方向夹角α从0°增加到180°的过程中，下列说法正确的是

A.小球B受到的合力的方向始终沿着轻杆A指向轴O

B.当α=90°时小球B受到轻杆A的作用力方向竖直向上

C.轻杆A对小球B做负功

D.小球B重力做功的功率不断增大

【答案】AC

【解析】

试题分析：小球做匀速圆周运动，所以受到的合力一定指向圆心O，A正确；当α=90°时小球B受到竖直向下的重力以及杆给的弹力，两力的合力一定指向圆心，故小球B受到轻杆A的作用力方向一定不会在竖直方向上，B错误；由于过程中，动能不变，机械能减小，所以杆对小球做负功，C正确；从0°增加到180°的过程中小球竖直方向上方的速度分量，先增大后减小，故重力的功率先增大后减小，D错误；

考点：考查了圆周运动，功率的计算

【题型】单选题
【结束】
86

【题目】如图所示，理想变压器原、副线圈的匝数比为10∶1，原线圈接交流电源和交流电压表、交流电流表，副线圈通过电阻为R的导线与热水器、抽油烟机连接．已知原线圈两端的电压保持不变，副线圈上的电压按如图乙所示规律变化．现闭合开关S接通抽油烟机，下列说法正确的是(　　)

A. 热水器两端电压的瞬时值表达式为u＝220sin(100πt)V

B. 电压表示数为2 200 V

C. 电流表示数变大

D. 变压器的输入功率增大

【题目】如图所示，位于坐标原点O处的振源由t＝0时刻开始向上起振，在沿x轴的正方向上形成一列简谐横波，质点A、B、C、D是其传播方向上的四点，且满足OA＝AB＝BC＝CD，经时间t＝0.3s的时间该波刚好传播到质点C处，此刻振源O第一次处于波谷位置．则下列说法正确的是______．

A．该振源的振动周期为T＝0.4s

B．在t＝0.3s时质点A处在平衡位置且向上振动

C．在t＝0.3s时质点B处在波谷位置

D．当该波刚传到质点D时，质点D的振动方向向上

E．在t＝0.5s时质点C处在平衡位置且向下振动

【答案】ADE

【解析】由于振源的起振方向向上，且在t=0.3 s时，该波刚好传播到质点C处，此刻振源O第一次处于波谷位置，则可知T=0.4 s，波长λ=4OA，A正确；据此时波形可知，该时刻质点A处在平衡位置且向下振动，质点B处在波峰位置，B、C错误；各质点的起振方向与波源的起振方向相同，故质点D的起振方向向上，D正确；t=0.5 s时该波向右传播的距离为，由波的传播可知此刻的质点C正处在平衡位置且向下振动，E正确．

【题型】填空题
【结束】
81

【题目】下列说法正确的是（）

A．平均速度、瞬时速度以及加速度，都是牛顿首先建立起来的

B．绕太阳运行的8颗行星中，海王星被人们称为“笔尖下发现的行星”

C．元电荷、点电荷等，都是由美国科学家富兰克林命名的

D．使用多用电表测电阻时，如果发现指针偏转很小，应选择倍率较小的欧姆档重新测量

【题目】如图所示，质量为m的小球用细线拴住放在光滑斜面上，斜面足够长，倾角为α的斜面体置于光滑水平面上，用水平力F推斜面体使斜面体缓慢地向左移动，小球沿斜面缓慢升高。当线拉力最小时，推力F等于

A. mgsin α B. mgsin α

C. mgsin 2α D. mgsin 2α

【题目】一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图所示，质点P的x坐标为3 m。已知任意振动质点连续2次经过平衡位置的时间间隔为0.4 s。下列说法正确的是________。

A．波速为1 m/s

B．波的频率为1.25 Hz

C．x坐标为15 m的质点在t＝0.6 s时恰好位于波峰

D．x坐标为22 m的质点在t＝0.2 s时恰好位于波峰

E．当质点P位于波峰时，x坐标为17 m的质点恰好位于波谷

【题目】如图甲所示，在平行虚线MN、PQ间有垂直于纸面的交变磁场，两虚线间的距离为d，磁场的磁感应强度随时间变化的规律如图乙所示，磁场变化的周期为T.一质量为m、电荷量为q的带电粒子在虚线MN上的A点以垂直于MN向右射入两虚线间，若磁场的磁感应强度，不计粒子的重力，则下列说法正确的是

A. 粒子在磁场中做圆周运动的周期也为T

B. 粒子在时刻射入，粒子会从虚线MN射出

C. 要使粒子在两虚线间能做一个完整的圆周运动，粒子的速度最大可以为

D. 要使粒子在两虚线间能做两个完整的圆周运动，粒子的速度最大可以为

【题目】如图所示，在平面直角坐标系xOy的第二、第三象限内有一垂直纸面向里、磁感应强度为B的匀强磁场区域△ABC，A点坐标为（0，3a），C点坐标为（0，﹣3a），B点坐标为(，-3a）．在直角坐标系xOy的第一象限内，加上方向沿y轴正方向、场强大小为E=Bv0的匀强电场，在x=3a处垂直于x轴放置一平面荧光屏，其与x轴的交点为Q．粒子束以相同的速度v0由O、C间的各位置垂直y轴射入，已知从y轴上y=﹣2a的点射入磁场的粒子在磁场中的轨迹恰好经过O点．忽略粒子间的相互作用，不计粒子的重力．

（1）求粒子的比荷；

（2）求粒子束射入电场的纵坐标范围；

（3）从什么位置射入磁场的粒子打到荧光屏上距Q点最远？求出最远距离．

试题分类