题目内容
10.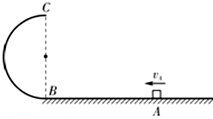 如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.质量m=0.40kg小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA=6.0m/s.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.10m.取重力加速度g=10m/s2.求:
如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.质量m=0.40kg小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA=6.0m/s.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.10m.取重力加速度g=10m/s2.求:(1)滑块运动到B点时速度的大小vB;
(2)滑块运动到B点时对轨道的压力;
(3)试计算分析滑块能否经C点水平飞出.
分析 (1)从A到B利用动能定理即可求解vB.
(2)在B点,由重力和轨道的支持力的合力提供向心力,根据牛顿运动定律求解.
(3)从B到C,利用机械能守恒定律求解滑块到达C点的速度,再与临界速度比较分析即可.
解答 解:(1)滑块从A到B,由动能定理,得:
-μmgL=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{A}^{2}$
解得 vB=5 m/s
(2)在B点,由牛顿运动定律得
$F-mg=m\frac{v_B^2}{R}$
解得 F=29N
由牛顿第三定律,对轨道压力F压=F=29N
(3)设滑块能通过C点,则由机械能守恒得
$\frac{1}{2}mv_B^2=\frac{1}{2}mv_c^2+mg•2R$
解得:vc=3m/s
若恰好能通过最高点,在C点速度为v,则有 $mg=m\frac{v^2}{R}$
解得 $v=\sqrt{gR}=2m/s$
因 vC>v,故滑块可以通过C点飞出
答:
(1)滑块运动到B点时速度的大小vB是5m/s.
(2)滑块运动到B点时对轨道的压力是29N.
(3)滑块能经C点水平飞出.
点评 本题是典型题目,能熟练运用动能定理和机械能守恒定律,明确滑块通过最高点的速度求法.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
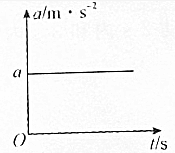
20. 如图所示,以8m/s的速度匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线25m.该车加速时最大加速度大小为3m/s2,减速时最大加速度大小为4m/s2.此路段允许行驶的最大速度为12.5m/s,下列关于汽车的说法正确的是( )
如图所示,以8m/s的速度匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线25m.该车加速时最大加速度大小为3m/s2,减速时最大加速度大小为4m/s2.此路段允许行驶的最大速度为12.5m/s,下列关于汽车的说法正确的是( )
 如图所示,以8m/s的速度匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线25m.该车加速时最大加速度大小为3m/s2,减速时最大加速度大小为4m/s2.此路段允许行驶的最大速度为12.5m/s,下列关于汽车的说法正确的是( )
如图所示,以8m/s的速度匀速行驶的汽车即将通过路口,绿灯还有2s将熄灭,此时汽车距离停车线25m.该车加速时最大加速度大小为3m/s2,减速时最大加速度大小为4m/s2.此路段允许行驶的最大速度为12.5m/s,下列关于汽车的说法正确的是( )| A. | 若立即做匀加速运动,在绿灯熄灭前可能通过停车线 | |
| B. | 若立即做匀加速运动,在绿灯熄灭前通过停车线一定超速 | |
| C. | 若在距停车线9m处开始减速,能停在停车线处 | |
| D. | 无论立即加速还是立即减速,都会违反交通规则 |
1.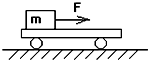 如图在光滑水平面上放一长为L的小车,车的左端有一质量m的木块,两者间动摩擦因数为μ.当物体在水平力F作用下从左端滑至右端时,在车固定和可自由滑动的两情况下( )
如图在光滑水平面上放一长为L的小车,车的左端有一质量m的木块,两者间动摩擦因数为μ.当物体在水平力F作用下从左端滑至右端时,在车固定和可自由滑动的两情况下( )
 如图在光滑水平面上放一长为L的小车,车的左端有一质量m的木块,两者间动摩擦因数为μ.当物体在水平力F作用下从左端滑至右端时,在车固定和可自由滑动的两情况下( )
如图在光滑水平面上放一长为L的小车,车的左端有一质量m的木块,两者间动摩擦因数为μ.当物体在水平力F作用下从左端滑至右端时,在车固定和可自由滑动的两情况下( )| A. | 两次物体所受的摩擦力相同 | B. | 两次力F所做的功相同 | ||
| C. | 因摩擦消耗的机械能相同 | D. | 物体获得的动能相同 |
18. 载人航天器在发射和降落时,宇航员会发生黑视,其原因一是因血压降低,二是因为大脑缺血.为此,航天器的气密舱有特殊的设计,如图所示,它固定在一个横轴上,可绕轴做360°旋转,这样设计的目的是( )
载人航天器在发射和降落时,宇航员会发生黑视,其原因一是因血压降低,二是因为大脑缺血.为此,航天器的气密舱有特殊的设计,如图所示,它固定在一个横轴上,可绕轴做360°旋转,这样设计的目的是( )
 载人航天器在发射和降落时,宇航员会发生黑视,其原因一是因血压降低,二是因为大脑缺血.为此,航天器的气密舱有特殊的设计,如图所示,它固定在一个横轴上,可绕轴做360°旋转,这样设计的目的是( )
载人航天器在发射和降落时,宇航员会发生黑视,其原因一是因血压降低,二是因为大脑缺血.为此,航天器的气密舱有特殊的设计,如图所示,它固定在一个横轴上,可绕轴做360°旋转,这样设计的目的是( )| A. | 宇航员舒适些 | B. | 宇航员始终承受横向加速度 | ||
| C. | 宇航员始终承受负加速度 | D. | 宇航员始终承受正加速度 |
5. 转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
 转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
转笔(Pen Spinning)是一项用不同的方法与技巧、以手指来转动笔的休闲活动,如图所示.转笔深受广大中学生的喜爱,其中也包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )| A. | 笔杆上的点离O点越近的,做圆周运动的角速度越大 | |
| B. | 笔杆上的点离O点越近的,做圆周运动的向心加速度越大 | |
| C. | 笔杆做圆周运动的向心力是由万有引力提供的 | |
| D. | 若该同学使用中性笔,墨汁可能会因笔快速的转动做离心运动被甩出 |
15.一蹦极运动员身系弹性蹦极绳从水面上方的高台下落,到最低点时距水面还有数米距离.假定空气阻力可忽略,运动员可视为质点,下列说法正确的是( )
| A. | 运动员到达最低点前重力势能始终减小 | |
| B. | 蹦极过程中,重力势能的改变与重力势能零点的选取有关 | |
| C. | 蹦极过程中,运动员、地球和蹦极绳所组成的系统机械能守恒 | |
| D. | 蹦极绳张紧后的下落过程中,弹性力做负功,弹性势能增加 |
2.根据热力学第二定律,下列判断正确的是( )
| A. | 热机中,燃气内能不可能全部转化为机械能 | |
| B. | 一个物体的机械能不可能全部转化为内能 | |
| C. | 在火力发电机中,燃气的内能可以全部转化为电能 | |
| D. | 在热传导中,热量不可能自发地从低温物体传递给高温物体 |