题目内容
9.质量为2kg的物块沿倾角为30°的粗糙斜面匀加速下滑,已知斜面长10m,物块由斜面顶端滑到底端经过5s,如果由摩擦损失的机械能全部转变成了内能,求在这一过程中物块与斜面系统的内能增加量.(g=10m/s2)分析 物体沿斜面向下做加速运动,由运动学的公式求出加速度,然后结合受力分析和牛顿第二定律即可求解摩擦力,系统内能的增量等于物体克服摩擦阻力做的功,即Q=f•△S.
解答 解:物体沿斜面向下运动的过程中,受到重力、斜面的支持力和摩擦力的作用,沿斜面向下加速,则:
L=$\frac{1}{2}a{t}^{2}$
所以有:a=$\frac{2L}{{t}^{2}}=\frac{2×10}{{5}^{2}}=0.8m/{s}^{2}$
沿斜面的方向有:mgsin30°-f=ma
代入数据得:f=8.4N
由于系统内能的增量等于物体克服摩擦阻力做的功.所以有:△E=Wf=fL=8.4×10=84J
答:系统增加的内能是84J.
点评 本题关键明确一对滑动摩擦力做的功之和等于内能的增加量,即Q=△E=f•△S.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.关于重心的说法,正确的是( )
| A. | 物体的重心一定在物体上 | |
| B. | 形状规则的物体的重心一定在其几何中心上 | |
| C. | 用一根细线悬挂的静止物体,细线方向一定通过物体的重心 | |
| D. | 物体重心的位置不仅跟物体的质量分布情况有关,而且还跟物体的形状有关 |
14.下列说法中正确的是 ( )
| A. | 物体在恒力作用下一定做直线运动 | |
| B. | 物体在恒力作用下一定做曲线运动 | |
| C. | 若物体的速度方向和加速度方向总在同一直线上,则该物体可能做曲线运动 | |
| D. | 物体在恒力作用下不可能做匀速圆周运动 |
1.两个形状完全相同的金属球,带电荷量分别为-2×10-9C和+6×10-9C,它们之间的静电力为F.在绝缘条件下,让它们接触后又放回原处,它们之间的静电力大小等于( )
| A. | F | B. | $\frac{4}{3}$F | C. | $\frac{3}{4}$F | D. | $\frac{1}{3}$F |
19. 等腰梯形导线框从位于匀强磁场上方一定高度处自由下落,已知下落过程两平行边始终竖直,左平行边长为a,右平行边长为2a.从导线框进入磁场开始计时,位移为$\frac{a}{2}$时,导线框做匀速运动.则从导线框刚进入磁场开始,下列判断正确的是( )
等腰梯形导线框从位于匀强磁场上方一定高度处自由下落,已知下落过程两平行边始终竖直,左平行边长为a,右平行边长为2a.从导线框进入磁场开始计时,位移为$\frac{a}{2}$时,导线框做匀速运动.则从导线框刚进入磁场开始,下列判断正确的是( )
 等腰梯形导线框从位于匀强磁场上方一定高度处自由下落,已知下落过程两平行边始终竖直,左平行边长为a,右平行边长为2a.从导线框进入磁场开始计时,位移为$\frac{a}{2}$时,导线框做匀速运动.则从导线框刚进入磁场开始,下列判断正确的是( )
等腰梯形导线框从位于匀强磁场上方一定高度处自由下落,已知下落过程两平行边始终竖直,左平行边长为a,右平行边长为2a.从导线框进入磁场开始计时,位移为$\frac{a}{2}$时,导线框做匀速运动.则从导线框刚进入磁场开始,下列判断正确的是( )| A. | 在0~$\frac{a}{2}$这段位移内,导线框可能做匀加速运动 | |
| B. | 在$\frac{a}{2}$~$\frac{3a}{2}$这段位移内,导线框减少的重力势能最终全部转化为内能 | |
| C. | 在$\frac{3a}{2}$~2a这段位移内,导线框可能做减速运动 | |
| D. | 在0~$\frac{a}{2}$与$\frac{3a}{2}$~2a位移内,导线框受到的安培力方向相同 |
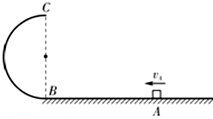 如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.质量m=0.40kg小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA=6.0m/s.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.10m.取重力加速度g=10m/s2.求:
如图所示,竖直平面内的半圆形轨道下端与水平面相切,B、C分别为半圆形轨道的最低点和最高点.质量m=0.40kg小滑块(可视为质点)沿水平面向左滑动,经过A点时的速度vA=6.0m/s.已知半圆形轨道光滑,半径R=0.40m,滑块与水平面间的动摩擦因数μ=0.50,A、B两点间的距离L=1.10m.取重力加速度g=10m/s2.求: 传感器是自动化控制中的重要元件,作用是将非电学量 (加速度、速度、位移等)转换为电学量(电压.电流等).以便实现自动控制,如图所示的位移传感器.当被测物体在左右方向发生位移时,电介质板随之在电容器两极板之间移动,如果测出电容的变化,就能知道位移动的变化.若电容器的电容变小.则物体可能是加速向右移动,也可能是减速向右移动,也可能是匀速向右移动.(选填“左”或“右”)
传感器是自动化控制中的重要元件,作用是将非电学量 (加速度、速度、位移等)转换为电学量(电压.电流等).以便实现自动控制,如图所示的位移传感器.当被测物体在左右方向发生位移时,电介质板随之在电容器两极板之间移动,如果测出电容的变化,就能知道位移动的变化.若电容器的电容变小.则物体可能是加速向右移动,也可能是减速向右移动,也可能是匀速向右移动.(选填“左”或“右”) 木块质量为m,放在水面上静止(平衡),如图所示;今用力向下将其压入水中一段深度后撤掉外力,木块在水面上振动,试判别木块的振动是否为简谐运动.
木块质量为m,放在水面上静止(平衡),如图所示;今用力向下将其压入水中一段深度后撤掉外力,木块在水面上振动,试判别木块的振动是否为简谐运动.