题目内容
1．
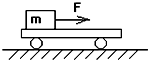如图在光滑水平面上放一长为L的小车，车的左端有一质量m的木块，两者间动摩擦因数为μ．当物体在水平力F作用下从左端滑至右端时，在车固定和可自由滑动的两情况下（ ）| A． | 两次物体所受的摩擦力相同 | B． | 两次力F所做的功相同 | ||
| C． | 因摩擦消耗的机械能相同 | D． | 物体获得的动能相同 |
分析 滑动摩擦力根据公式f=μN分析．根据位移关系分析力F做功关系．根据Q=f•△s，△s是相对位移分析消耗的机械能关系．根据运动学公式分析速度的关系，从而得到动能关系．
解答 解：A、物体所受的摩擦力都是滑动摩擦力，大小为 f=μN=μmg，可知摩擦力相同，故A正确．
B、车不固定时m相对于地的位移大，由W=Fs知车不固定时力F做功多，故B错误．
C、因摩擦消耗的机械能等于f•△s=fL，L是车的长度，可知因摩擦消耗的机械能相同，故C正确．
D、两次m的受力情况相同，加速度相同，车不固定时所用时间长，由v=at知，车不固定时物体获得的速度大，动能也大，故D错误．
故选：AC．
点评 本题是木块在小车滑动的类型，采用隔离法进行研究，要正确分析物体的受力情况，关键要抓住相对位移分析消耗的机械能，运用运动学公式和牛顿第二定律结合进行分析．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
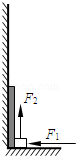示，一长L=0.8m、质量M=0.4kg的木板靠在光滑竖直墙面上，木板右下方有一质量m=0.8kg的小滑块（可视为质点），滑块与木板间的动摩擦因数为μ=0.2，滑块与木板间的最大静摩擦力等于滑动摩擦力，取g=10m/s2．一人用水平恒力F1向左作用在滑块上，另一人用竖直恒力F2向上拉动滑块，使滑块从地面由静止开始向上运动．
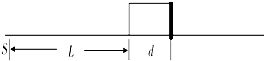如图所示，在一块厚平面平行玻璃砖（后面镀银）前面距离L处有一点光源S．已知玻璃砖的厚度为d，折射率为n，高度相对厚度较小．试求该点光源成像的位置．
有一半径为R的半圆形光滑绝缘槽，置于水平向右的匀强电场中，若把一个带正电的小球放置在槽的B点时（OB与竖直方向成37°角）刚好静止，若使小球从槽的边缘A点由静止滑下，求
如图所示，一质点先从A运动到B，再从B运动到C．
13．（多选）设地面附近重力加速度为g，地球半径为R0，人造地球卫星圆形运行轨道半径为R，那么以下说法正确的是（ ）
| A． | 卫星在轨道上向心加速度大小为$\frac{R_0^2}{R^2}g$ | |
| B． | 卫星在轨道上运行速度大小为$\sqrt{\frac{R_0^2g}{R}}$ | |
| C． | 卫星运行的角速度大小为$\sqrt{\frac{R^3}{R_0^2g}}$ | |
| D． | 卫星运行的周期为$2π\sqrt{\frac{R^3}{R_0^2g}}$ |
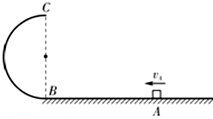如图所示，竖直平面内的半圆形轨道下端与水平面相切，B、C分别为半圆形轨道的最低点和最高点．质量m=0.40kg小滑块（可视为质点）沿水平面向左滑动，经过A点时的速度vA=6.0m/s．已知半圆形轨道光滑，半径R=0.40m，滑块与水平面间的动摩擦因数μ=0.50，A、B两点间的距离L=1.10m．取重力加速度g=10m/s2．求：
传感器是自动化控制中的重要元件，作用是将非电学量 （加速度、速度、位移等）转换为电学量（电压．电流等）．以便实现自动控制，如图所示的位移传感器．当被测物体在左右方向发生位移时，电介质板随之在电容器两极板之间移动，如果测出电容的变化，就能知道位移动的变化．若电容器的电容变小．则物体可能是加速向右移动，也可能是减速向右移动，也可能是匀速向右移动．（选填“左”或“右”）