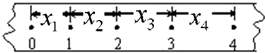
��Ŀ����
9��һ�����������������߶ȵ��ڵ���뾶��Բ�ι�������У���֪gΪ���������������ٶȣ�����ĵ�һ�����ٶ���v1��������˵����ȷ���ǣ�������| A�� | ����������е����ٶ�Ϊ$\sqrt{2}$v1 | |
| B�� | ���Ƶ����˶������ļ��ٶ�Ϊ$\frac{1}{4}$g | |
| C�� | ����Ϊm���������������ڵ�ƽ̨�ϣ�������ƽ̨��ѹ��Ϊ$\frac{1}{4}$mg | |
| D�� | �������������ϼ��ٺ��ʵ����ͬ�����ǶԽ� |
���� ����ĵ�һ�����ٶ��ǵ��������Ƶ����˶�������ٶȣ�������������е����ٶ�С��v1����ţ�ٵڶ����ɺ�������������������ʽ��������ļ��ٶȣ�
������������������������ʽ�õ��������ܵ����������Ǵ���ʧ��״̬��������ƽ̨��ѹ��Ϊ�㣮
��� �⣺A������ĵ�һ�����ٶ��ǵ��������Ƶ����˶�������ٶȣ�������������е����ٶ�С��v1����A����
B���ڵ�����棬���������ṩ�������ã�
$G\frac{Mm}{{R}^{2}}=mg$��
�������������������ṩ�����������У�
$G\frac{Mm}{{��R+R��}^{2}}=ma$
��ã�a=$\frac{1}{4}g$����B��ȷ��
C����Բ������У�������ȫʧ��״̬����ѹ��Ϊ�㣬��C����
D�������뾶С��ͬ�����ǹ����Ҫ���ٲſɵ���ͬ�����ʵ�ֶԽӣ���D��ȷ��
��ѡ��BD
���� ����Ϊ������Բ���˶��Ļ�����������Ŀ����Ҫ�������������䵱�����������������������������Ӧ�úͼ��㣮

��ϰ��ϵ�д�
 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
�����Ŀ
17��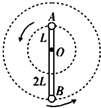 ��ͼ��ʾ����˳�Ϊ3L���ڸ˵�A��B���˷ֱ�̶�������Ϊm����A����B�����Ͼ���AΪL���ĵ�Oװ�ڹ⻬��ˮƽת�����ϣ�������ϵͳһ���������˺�������ֱ����ת������ת���Ĺ����У����Կ���������������B�˶�����ߵ�ʱ����B�Ը�ǡ������������������˵����ȷ���ǣ�������
��ͼ��ʾ����˳�Ϊ3L���ڸ˵�A��B���˷ֱ�̶�������Ϊm����A����B�����Ͼ���AΪL���ĵ�Oװ�ڹ⻬��ˮƽת�����ϣ�������ϵͳһ���������˺�������ֱ����ת������ת���Ĺ����У����Կ���������������B�˶�����ߵ�ʱ����B�Ը�ǡ������������������˵����ȷ���ǣ�������
 ��ͼ��ʾ����˳�Ϊ3L���ڸ˵�A��B���˷ֱ�̶�������Ϊm����A����B�����Ͼ���AΪL���ĵ�Oװ�ڹ⻬��ˮƽת�����ϣ�������ϵͳһ���������˺�������ֱ����ת������ת���Ĺ����У����Կ���������������B�˶�����ߵ�ʱ����B�Ը�ǡ������������������˵����ȷ���ǣ�������
��ͼ��ʾ����˳�Ϊ3L���ڸ˵�A��B���˷ֱ�̶�������Ϊm����A����B�����Ͼ���AΪL���ĵ�Oװ�ڹ⻬��ˮƽת�����ϣ�������ϵͳһ���������˺�������ֱ����ת������ת���Ĺ����У����Կ���������������B�˶�����ߵ�ʱ����B�Ը�ǡ������������������˵����ȷ���ǣ�������| A�� | ��B����ߵ�ʱ�ٶ�Ϊ�� | B�� | ��B����ߵ�ʱ����A���ٶ�Ϊ$\frac{\sqrt{2gL}}{2}$ | ||
| C�� | ��Bת����͵�ʱ�����ٶ�Ϊ$\sqrt{\frac{26}{5}gL}$ | D�� | ��Bת����͵�ʱ�����ٶ�Ϊ$\sqrt{\frac{16}{5}gL}$ |
4��ij����10N����������б�潫��Ϊ16N���������ٵ����ϳ�Ϊ4m����Ϊ2m��б�涥�ˣ���б��Ļ�еЧ�ʦǼ�б��������Ħ����f��С�ֱ�Ϊ��������
| A�� | ��=0.5��f=8 N | B�� | ��=0.5��f=2 N | C�� | ��=0.8��f=2 N | D�� | ��=0.8��f=8 N |
14����֪A��B�ǵ�һ��������Ķ�����Ԫ�أ����ǿ����γ����ӻ�����AmBn���ڴ˻������У��������Ӿ����γ�ϡ������ԭ�ӵ��ȶ��ṹ����A�ĺ˵����Ϊa����B�ĺ˵�����������ǣ�������
| A�� | a+8-m-n | B�� | a+18-m-n | C�� | a+16-m-n | D�� | a-m-n |
1�� ��б��픶�ˮƽ�׳�һ����Ϊ�ʵ��С��С������б���ϣ���֪б��������37�㣬��ͼ��ʾ�������ǿ����������������ж���ȷ���ǣ�������
��б��픶�ˮƽ�׳�һ����Ϊ�ʵ��С��С������б���ϣ���֪б��������37�㣬��ͼ��ʾ�������ǿ����������������ж���ȷ���ǣ�������
 ��б��픶�ˮƽ�׳�һ����Ϊ�ʵ��С��С������б���ϣ���֪б��������37�㣬��ͼ��ʾ�������ǿ����������������ж���ȷ���ǣ�������
��б��픶�ˮƽ�׳�һ����Ϊ�ʵ��С��С������б���ϣ���֪б��������37�㣬��ͼ��ʾ�������ǿ����������������ж���ȷ���ǣ�������| A�� | ������׳��������֮��ľ��룬���������С��ij��ٶ� | |
| B�� | С����б�����Զ�����˶��켣���е� | |
| C�� | ������С���׳����ٶȣ���������С���䵽б��ʱ���ٶ���б��ļн� | |
| D�� | ��С����ƽ���˶���ʱ��Ϊt������$\frac{t}{2}$ʱ��С����б����Զ |
18��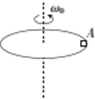 ��ͼ��ʾ��Բ������ֱ������ת����������ظ߶�Ϊh����ת���Ľ��ٶ�Ϊ��0ʱ��λ��Բ�̱�Ե�����A���ɿ����ʵ㣩�պô�Բ���Ϸ��룬�ӷɳ�����صģ�ˮƽλ�Ƹպ�Ϊh�����ƿ������������������Բ�̵����Ħ�������ڻ���Ħ��������������
��ͼ��ʾ��Բ������ֱ������ת����������ظ߶�Ϊh����ת���Ľ��ٶ�Ϊ��0ʱ��λ��Բ�̱�Ե�����A���ɿ����ʵ㣩�պô�Բ���Ϸ��룬�ӷɳ�����صģ�ˮƽλ�Ƹպ�Ϊh�����ƿ������������������Բ�̵����Ħ�������ڻ���Ħ��������������
 ��ͼ��ʾ��Բ������ֱ������ת����������ظ߶�Ϊh����ת���Ľ��ٶ�Ϊ��0ʱ��λ��Բ�̱�Ե�����A���ɿ����ʵ㣩�պô�Բ���Ϸ��룬�ӷɳ�����صģ�ˮƽλ�Ƹպ�Ϊh�����ƿ������������������Բ�̵����Ħ�������ڻ���Ħ��������������
��ͼ��ʾ��Բ������ֱ������ת����������ظ߶�Ϊh����ת���Ľ��ٶ�Ϊ��0ʱ��λ��Բ�̱�Ե�����A���ɿ����ʵ㣩�պô�Բ���Ϸ��룬�ӷɳ�����صģ�ˮƽλ�Ƹպ�Ϊh�����ƿ������������������Բ�̵����Ħ�������ڻ���Ħ��������������| A�� | Բ�̵İ뾶Ϊ$\frac{\sqrt{2gh}}{2{��}_{0}}$ | B�� | Բ�̵İ뾶Ϊ$\frac{\sqrt{2gh}}{{��}_{0}}$ | ||
| C�� | �����Բ�̵Ķ�Ħ������Ϊ��0$\sqrt{\frac{h}{2g}}$ | D�� | �����Բ�̵Ķ�Ħ������Ϊ��0$\sqrt{\frac{2h}{g}}$ |

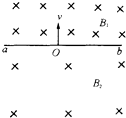 ��ͼ��ʾ����abΪ�ֽ����������ǿ�ų����������ֱ��ֽ�������Ÿ�Ӧǿ��B1=2B2������һ����Ϊm�������Ϊq�����Ӵ�O����ͼʾ�������ٶ�v�˶�������t1=$\frac{��m}{2q{B}_{2}}$ʱ�����ӵ�һ�λص�ab�ߣ�����t=$\frac{2��m}{q{B}_{2}}$��ʱ���������»ص�O�㣮
��ͼ��ʾ����abΪ�ֽ����������ǿ�ų����������ֱ��ֽ�������Ÿ�Ӧǿ��B1=2B2������һ����Ϊm�������Ϊq�����Ӵ�O����ͼʾ�������ٶ�v�˶�������t1=$\frac{��m}{2q{B}_{2}}$ʱ�����ӵ�һ�λص�ab�ߣ�����t=$\frac{2��m}{q{B}_{2}}$��ʱ���������»ص�O�㣮