题目内容
18.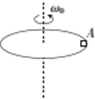 如图所示,圆盘绕竖直轴匀速转动,盘面离地高度为h,当转动的角速度为ω0时,位于圆盘边缘的物块A(可看成质点)刚好从圆盘上飞离,从飞出到落地的(水平位移刚好为h,不计空气阻力,则(假设物块与圆盘的最大静摩擦力等于滑动摩擦力)( )
如图所示,圆盘绕竖直轴匀速转动,盘面离地高度为h,当转动的角速度为ω0时,位于圆盘边缘的物块A(可看成质点)刚好从圆盘上飞离,从飞出到落地的(水平位移刚好为h,不计空气阻力,则(假设物块与圆盘的最大静摩擦力等于滑动摩擦力)( )| A. | 圆盘的半径为$\frac{\sqrt{2gh}}{2{ω}_{0}}$ | B. | 圆盘的半径为$\frac{\sqrt{2gh}}{{ω}_{0}}$ | ||
| C. | 物块与圆盘的动摩擦因数为ω0$\sqrt{\frac{h}{2g}}$ | D. | 物块与圆盘的动摩擦因数为ω0$\sqrt{\frac{2h}{g}}$ |
分析 物块从圆盘上飞离后做平抛运动,根据平抛运动基本公式结合v=ω0r求解半径,物块A刚好从圆盘上飞离,则由滑动摩擦力提供向心力列式即可求解动摩擦因数.
解答 解:A、物块从圆盘上飞离后做平抛运动,根据平抛运动基本公式得:
h=vt,
h=$\frac{1}{2}g{t}^{2}$,
而v=ω0r
解得:r=$\frac{\sqrt{2gh}}{2{ω}_{0}}$,故A正确,B错误.
C、物块A刚好从圆盘上飞离,则由滑动摩擦力提供向心力,则有:
μmg=mω0r
解得:$μ={ω}_{0}\sqrt{\frac{h}{2g}}$,故C正确,D错误.
故选:AC
点评 本题主要考查了平抛运动的基本规律,关键是对物体受力分析,然后根据合力提供向心力,运用牛顿第二定律列式求解即可.

练习册系列答案
相关题目
8.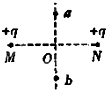 如图所示,将等量的正点电荷分别固定于M、N两点,O点为MN连线的中点,点a、b 在MN的中垂线上并关于O点对称.下列说法正确的是( )
如图所示,将等量的正点电荷分别固定于M、N两点,O点为MN连线的中点,点a、b 在MN的中垂线上并关于O点对称.下列说法正确的是( )
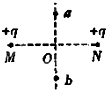 如图所示,将等量的正点电荷分别固定于M、N两点,O点为MN连线的中点,点a、b 在MN的中垂线上并关于O点对称.下列说法正确的是( )
如图所示,将等量的正点电荷分别固定于M、N两点,O点为MN连线的中点,点a、b 在MN的中垂线上并关于O点对称.下列说法正确的是( )| A. | a、b两点的电场强度相同 | |
| B. | a、b两点的电势相等 | |
| C. | 将电子沿直线从a点移到0点,所受电场力一定减小 | |
| D. | 一负电荷在此电场中经过a、b两点可能做匀速圆周运动 |
9.一颗人造卫星在离地面高度等于地球半径的圆形轨道上运行,已知g为地球表面的重力加速度,地球的第一宇宙速度是v1,则下列说法正确的是( )
| A. | 这颗卫星运行的线速度为$\sqrt{2}$v1 | |
| B. | 它绕地球运动的向心加速度为$\frac{1}{4}$g | |
| C. | 质量为m的仪器放在卫星内的平台上,仪器对平台的压力为$\frac{1}{4}$mg | |
| D. | 此卫星在其轨道上加速后可实现与同步卫星对接 |
13. 在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )
在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )
 在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )
在x轴上电场强度E与x的关系如图所示,O为坐标原点,a,c为x轴上的点,a,c之间的距离为d,a,c两点的电场强度大小为E0,则下列说法中正确的是( )| A. | φb>φa=φc>φo | |
| B. | φo>φa>φb>φc | |
| C. | 将质子从a点移到c点,电场力做功大于eE0d | |
| D. | 将质子由a点移到c点,质子的电势能增加 |
3.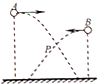 如图所示,A、B是高度不同的两点,A点比B点高,从A、B两点同时相向水平抛出两个小球M、N,其运动轨迹相交于P点,空气阻力不计.从抛出到落地的整个过程中,下列说法正确的是( )
如图所示,A、B是高度不同的两点,A点比B点高,从A、B两点同时相向水平抛出两个小球M、N,其运动轨迹相交于P点,空气阻力不计.从抛出到落地的整个过程中,下列说法正确的是( )
 如图所示,A、B是高度不同的两点,A点比B点高,从A、B两点同时相向水平抛出两个小球M、N,其运动轨迹相交于P点,空气阻力不计.从抛出到落地的整个过程中,下列说法正确的是( )
如图所示,A、B是高度不同的两点,A点比B点高,从A、B两点同时相向水平抛出两个小球M、N,其运动轨迹相交于P点,空气阻力不计.从抛出到落地的整个过程中,下列说法正确的是( )| A. | M小球先落地 | |
| B. | N小球先落地 | |
| C. | M、N两球在P点相遇 | |
| D. | M物体的速度变化量与N物体的速度变化量相同 |
10.质点作直线运动的v-t图象如图所示,则( )


| A. | 在第2秒末速度方向发生了改变 | B. | 2~4s内物体做匀减速直线运动 | ||
| C. | 在3s末质点的加速度为零 | D. | 第2秒末和第4秒末的位置相同 |
8.下列有关说法中正确的是( )
| A. | 质点是真实存在的 | |
| B. | 质点是一种忽略次要因素的理想化模型 | |
| C. | 研究汽车通过某一路标所用的时间时可以把汽车看作质点 | |
| D. | 坐标系的建立与参考系无关 |
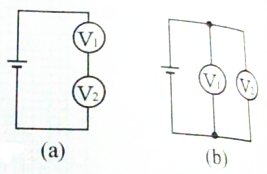 两只直流电压表V1和V2,接到一个内阻一定、电动势为E的直流电源上,按图(a)所示连接时,V1与V2的读数分别为2.0V和1.6V;按图(b)所示连接时,两表的读数均为2.0V,则V1与V2的内阻之比为5:4;V2内阻与电源内阻之比为5:4.
两只直流电压表V1和V2,接到一个内阻一定、电动势为E的直流电源上,按图(a)所示连接时,V1与V2的读数分别为2.0V和1.6V;按图(b)所示连接时,两表的读数均为2.0V,则V1与V2的内阻之比为5:4;V2内阻与电源内阻之比为5:4.