题目内容
3.光滑斜面长为L,一物体从斜面顶端由静止开始下滑,到达底端的速度为V,当物体的速度为$\frac{1}{2}$V时,它下滑距离为$\frac{L}{4}$,物体到达斜面中点位置时的运动时间为$\frac{\sqrt{2}L}{v}$.分析 根据匀变速直线运动的速度位移公式,求出物体速度为斜面底端速度一半时下滑的距离;
根据匀变速直线运动的速度位移公式,求出物体滑行距离是原来一半的时间.
解答 解:设到达底端的速度为v,根据速度位移公式得:
v2=2aL,
$(\frac{v}{2})^{2}=2as$,
联立两式解得:s=$\frac{L}{4}$.
由平均速度公式可得:
t=$\frac{2L}{v}$
根据速度位移公式得:
v2=2aL,
v′2=2a$•\frac{L}{2}$
解得:v′=$\frac{{\sqrt{2}}}{2}$v
由:v=at
v′=$\frac{{\sqrt{2}}}{2}$v=at′
可得:t′=$\frac{{\sqrt{2}}}{2}$t=$\frac{\sqrt{2}L}{v}$
故答案为:$\frac{L}{4}$,$\frac{\sqrt{2}L}{v}$
点评 本题考查初速度为0的匀加速直线运动的速度时间关系和位移速度关系,掌握规律是解决问题的关键,

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
14.下列几个关于力学问题的说法中正确的是( )
| A. | 米、千克、牛顿等都是国际单位制中的基本单位 | |
| B. | 同一物体运动快时和运动慢时惯性一样大 | |
| C. | 静止在水平面上的物体所受的重力与水平面给的支持力是一对相互作用力 | |
| D. | 放在斜面上的物体,其重力沿垂直斜面的分力就是物体对斜面的压力 |
8.根据最新官方消息,中国火星探测任务基本确定,发射时间大致在2018年左右,若火星探测器在登陆火星之前需在靠近火星表面绕火星做匀速圆周运动,已知引力常量为G,探测器在火星表面附近绕火星做匀速圆周运动的角速度为ω,则火星的平均密度为( )
| A. | $\frac{3{ω}^{2}}{4πG}$ | B. | $\frac{2{ω}^{2}}{3πG}$ | C. | $\frac{{ω}^{2}}{2πG}$ | D. | $\frac{{ω}^{2}}{4πG}$ |
 “百公里加速时间”是衡量一辆跑车性能的重要指标,如图所示,某跑车在平直公路上由静止加速至108km/h只需要3.0s时间,已知跑车的质量为2000kg,加速和减速过程均可以视作匀变速直线运动.
“百公里加速时间”是衡量一辆跑车性能的重要指标,如图所示,某跑车在平直公路上由静止加速至108km/h只需要3.0s时间,已知跑车的质量为2000kg,加速和减速过程均可以视作匀变速直线运动.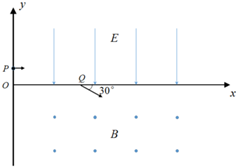 如图所示的xoy坐标系中,在第Ⅰ象限内存在沿y轴负向的匀强电场,第Ⅳ象限内存在垂直纸面向外的匀强磁场,一质量为m、电荷量为q的带正电粒子,从y轴上的P点垂直进入匀强电场,经过x轴上的Q点以速度v进入磁场,方向与x轴正向成30°.若粒子在磁场中运动后恰好能再回到电场,已知$\overrightarrow{OQ}$=3L,粒子的重力不计,电场强度E和磁感应强度B大小均求知,求
如图所示的xoy坐标系中,在第Ⅰ象限内存在沿y轴负向的匀强电场,第Ⅳ象限内存在垂直纸面向外的匀强磁场,一质量为m、电荷量为q的带正电粒子,从y轴上的P点垂直进入匀强电场,经过x轴上的Q点以速度v进入磁场,方向与x轴正向成30°.若粒子在磁场中运动后恰好能再回到电场,已知$\overrightarrow{OQ}$=3L,粒子的重力不计,电场强度E和磁感应强度B大小均求知,求

 如图所示为一列简谐波在t=0时刻的图象,已知质点M的振动方程为y=5sin5πt(cm),此波中质点M在t=0.9s时恰好第3次到达y轴正方向最大位移处,该波的波速1m/s.
如图所示为一列简谐波在t=0时刻的图象,已知质点M的振动方程为y=5sin5πt(cm),此波中质点M在t=0.9s时恰好第3次到达y轴正方向最大位移处,该波的波速1m/s. 为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超过弹簧的弹性限度.B弹簧的劲度系数为100N/m.劲度系数较大的是B(填A或B).
为了探究弹簧弹力F和弹簧伸长量x的关系,某同学选了A、B两根规格不同的弹簧进行测试,根据测得的数据绘出如图所示的图象,从图象上看,该同学没能完全按实验要求做,使图象上端成为曲线,图象上端成为曲线的原因是超过弹簧的弹性限度.B弹簧的劲度系数为100N/m.劲度系数较大的是B(填A或B).