题目内容
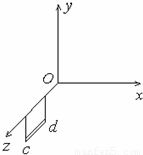
有一长为l=0.50m、质量10g的通电导线cd,由两根绝缘细线水平悬挂在匀强磁场中的z轴上,如图所示. z轴垂直纸面向外,g=10m/s2.求:(1)当磁感应强度B1=1.0T,方向与x 轴负方向相同时,要使悬线中张力为零,cd中的电流I1的大小和方向?
(2)当cd中通入方向由c到d的I2=0.40A的电流,这时磁感应强度B2=1.0T,方向与x轴正向相同,当cd静止时悬线中的张力是多大?
(3)当cd 通入方向由c到d的I3=0.10A的电流,若磁场方向垂直z轴,且与y轴负方向夹角为30°,与x轴正向夹角为60°,磁感应强度B3=2.0T,则导线cd静止时悬线中的张力又是多大?
【答案】分析:(1)根据磁场力与重力相平衡,与左手定则,从而即可求解;
(2)根据左手定则,与受力平衡,即可确定结果;
(3)根据安培力的大小与方向,及力的平行四边形定则,即可求解.
解答:解: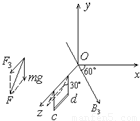 (1)要使悬线的张力为零,导线cd受到的磁场力必须与重力平衡,有F1=B1I1l,
(1)要使悬线的张力为零,导线cd受到的磁场力必须与重力平衡,有F1=B1I1l,
所以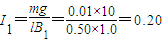 (A),
(A),
由左手定则可判定cd中的电流方向由c到d.
(2)根据题意,由左手定则可判定此时cd受到竖直向下的磁场力.
当cd静止时,有mg+B2I2l=2T,
所以 (N)
(N)
(3)根据题意,作出导线cd中点的受力如图所示.
这时cd受到的安培力大小为F3=B3I3l,
所以F3=0.10×0.50×2.0=0.10(N)=mg,
又因F3与B3垂直,因此F合与mg的夹角为30°.
所以T合=2T'=F合=2mgcos30°T'=mgcos30°=0.09(N)
此时每根悬线中的张力,其方向与y轴负方向的夹角为30°,
即导线cd受安培力作用后使悬线向x轴负方向偏转30°角.
答:(1)当磁感应强度B1=1.0T,方向与x 轴负方向相同时,要使悬线中张力为零,cd中的电流I1的大小0.2A和方向由c到d;
(2)当cd中通入方向由c到d的I2=0.40A的电流,这时磁感应强度B2=1.0T,方向与x轴正向相同,当cd静止时悬线中的张力是0.15N;
(3)当cd 通入方向由c到d的I3=0.10A的电流,若磁场方向垂直z轴,且与y轴负方向夹角为30°,与x轴正向夹角为60°,磁感应强度B3=2.0T,则导线cd受安培力作用后使悬线向x轴负方向偏转30°角.
点评:考查左手定则、安培力的大小公式,掌握受力分析及平衡方程,理解力的平行四边形定则的应用.
(2)根据左手定则,与受力平衡,即可确定结果;
(3)根据安培力的大小与方向,及力的平行四边形定则,即可求解.
解答:解:
 (1)要使悬线的张力为零,导线cd受到的磁场力必须与重力平衡,有F1=B1I1l,
(1)要使悬线的张力为零,导线cd受到的磁场力必须与重力平衡,有F1=B1I1l,所以
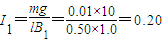 (A),
(A),由左手定则可判定cd中的电流方向由c到d.
(2)根据题意,由左手定则可判定此时cd受到竖直向下的磁场力.
当cd静止时,有mg+B2I2l=2T,
所以
 (N)
(N)(3)根据题意,作出导线cd中点的受力如图所示.
这时cd受到的安培力大小为F3=B3I3l,
所以F3=0.10×0.50×2.0=0.10(N)=mg,
又因F3与B3垂直,因此F合与mg的夹角为30°.
所以T合=2T'=F合=2mgcos30°T'=mgcos30°=0.09(N)
此时每根悬线中的张力,其方向与y轴负方向的夹角为30°,
即导线cd受安培力作用后使悬线向x轴负方向偏转30°角.
答:(1)当磁感应强度B1=1.0T,方向与x 轴负方向相同时,要使悬线中张力为零,cd中的电流I1的大小0.2A和方向由c到d;
(2)当cd中通入方向由c到d的I2=0.40A的电流,这时磁感应强度B2=1.0T,方向与x轴正向相同,当cd静止时悬线中的张力是0.15N;
(3)当cd 通入方向由c到d的I3=0.10A的电流,若磁场方向垂直z轴,且与y轴负方向夹角为30°,与x轴正向夹角为60°,磁感应强度B3=2.0T,则导线cd受安培力作用后使悬线向x轴负方向偏转30°角.
点评:考查左手定则、安培力的大小公式,掌握受力分析及平衡方程,理解力的平行四边形定则的应用.

练习册系列答案
相关题目
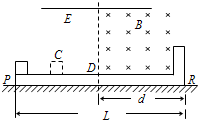 (2011?惠州二模)如图所示,一长为L=0.64m的绝缘平板PR固定在水平地面上,挡板只固定在平板右端.整个空间有一平行于PR的匀强电场E,在板的右半部分有一垂直纸面向里的匀强磁场B,磁场宽度d=0.32m.一质量m=O.50×10-3kg、电荷量q=5.0×l0-2 C的小物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动,碰到挡板R 后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),则物体返回时在磁场中仍做匀速运动,离开磁场后做减速运动且停在C点,PC=
(2011?惠州二模)如图所示,一长为L=0.64m的绝缘平板PR固定在水平地面上,挡板只固定在平板右端.整个空间有一平行于PR的匀强电场E,在板的右半部分有一垂直纸面向里的匀强磁场B,磁场宽度d=0.32m.一质量m=O.50×10-3kg、电荷量q=5.0×l0-2 C的小物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动,碰到挡板R 后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),则物体返回时在磁场中仍做匀速运动,离开磁场后做减速运动且停在C点,PC= (2005?海淀区一模)如图所示,PR是一长为L=0.64m的绝缘平板固定在水平地面上,挡板R固定在平板的右端.整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂于纸面向里的匀强磁场B,磁场的宽度为d=0.32m,一个质量为m=0.50×10-3kg、带电荷量为q=5.0×10-2C的物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动.物体碰到挡板R后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),物体返回时在磁场中仍作匀速运动,离开磁场后做减速运动,停在C点,PC=L/4,物体与平板间的动摩擦因数μ=0.20,g取10m/s2.求:
(2005?海淀区一模)如图所示,PR是一长为L=0.64m的绝缘平板固定在水平地面上,挡板R固定在平板的右端.整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂于纸面向里的匀强磁场B,磁场的宽度为d=0.32m,一个质量为m=0.50×10-3kg、带电荷量为q=5.0×10-2C的物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动.物体碰到挡板R后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),物体返回时在磁场中仍作匀速运动,离开磁场后做减速运动,停在C点,PC=L/4,物体与平板间的动摩擦因数μ=0.20,g取10m/s2.求:

