题目内容
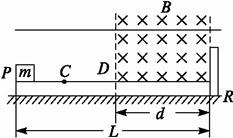
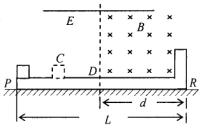
如图14所示,PR是一长为L=0.64 m 的绝缘平板,固定在水平地面上,挡板R固定在平板的右端.整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂直于纸面向里的匀强磁场B,磁场的宽度为0.32 m.一个质量m=0.50×10-3 kg、带电荷量q=5.0×102 C的小物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动.当物体碰到挡板R后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),物体返回时在磁场中仍做匀速运动,离开磁场后做减速运动,停在C点,PC=L/4.若物体与平板间的动摩擦因数μ=0.20,取g=10 m/s2.

图14
(1)判断电场的方向及物体带正电还是带负电;?
(2)求磁感应强度B的大小;?
(3)求物体与挡板碰撞过程中损失的机械能.
(1)电场方向向左 物体带负电 (2)0.13 T (3)4.8×10-4 J?
解析:
(1)物体由静止开始向右做匀加速运动,证明电场力向右且大于摩擦力.进入磁场后做匀速直线运动,说明它受的摩擦力增大,证明它受的洛伦兹力方向向下.由左手定则判断,物体带负电.物体带负电而所受电场力向右,证明电场方向向左.?
(2)设物体被挡板弹回后做匀速直线运动的速度为v2,从离开磁场到停止的过程中,根据动能定理有-μmg![]() =0-
=0-![]() mv22,解得v2=0.80 m/s.物体在磁场中向左做匀速直线运动,受力平衡,mg=qv2B,解得B≈0.125 T≈0.13 T.?
mv22,解得v2=0.80 m/s.物体在磁场中向左做匀速直线运动,受力平衡,mg=qv2B,解得B≈0.125 T≈0.13 T.?
(3)设从D点进入磁场时的速度为v1,根据动能定理有:qE![]() L-μmg
L-μmg![]() L=
L=![]() mv12,物体从D到R做匀速直线运动,受力平衡:qE=μ(mg+qv1B),解得v1=1.6 m/s,小物体撞击挡板损失的机械能:ΔE=
mv12,物体从D到R做匀速直线运动,受力平衡:qE=μ(mg+qv1B),解得v1=1.6 m/s,小物体撞击挡板损失的机械能:ΔE=![]() mv12-
mv12-![]() mv22,解得?ΔE=4.8×10-4 J.?
mv22,解得?ΔE=4.8×10-4 J.?

 活力课时同步练习册系列答案
活力课时同步练习册系列答案