题目内容
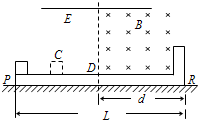 (2011?惠州二模)如图所示,一长为L=0.64m的绝缘平板PR固定在水平地面上,挡板只固定在平板右端.整个空间有一平行于PR的匀强电场E,在板的右半部分有一垂直纸面向里的匀强磁场B,磁场宽度d=0.32m.一质量m=O.50×10-3kg、电荷量q=5.0×l0-2 C的小物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动,碰到挡板R 后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),则物体返回时在磁场中仍做匀速运动,离开磁场后做减速运动且停在C点,PC=
(2011?惠州二模)如图所示,一长为L=0.64m的绝缘平板PR固定在水平地面上,挡板只固定在平板右端.整个空间有一平行于PR的匀强电场E,在板的右半部分有一垂直纸面向里的匀强磁场B,磁场宽度d=0.32m.一质量m=O.50×10-3kg、电荷量q=5.0×l0-2 C的小物体,从板的P端由静止开始向右做匀加速运动,从D点进入磁场后恰能做匀速直线运动,碰到挡板R 后被弹回,若在碰撞瞬间撤去电场(不计撤掉电场对原磁场的影响),则物体返回时在磁场中仍做匀速运动,离开磁场后做减速运动且停在C点,PC=| L | 4 |
(1)判断电场的方向及物体所带电荷的性质;
(2)求磁感应强度B的大小;
(3)求物体与挡板碰撞过程中损失的机械能.
分析:(1)由物体的运动状态可知粒子受到的电场力方向,由洛仑兹力可判断粒子的电性,则可得出电场方向;
(2)由动能定理可求得物体被弹回时的速度,由磁场中的受力平衡可求得磁感应强度;
(3)由动能定理及受力平衡关系联立可求得粒子进入磁场时的速度,由功能关系可求得损失的机械能.
(2)由动能定理可求得物体被弹回时的速度,由磁场中的受力平衡可求得磁感应强度;
(3)由动能定理及受力平衡关系联立可求得粒子进入磁场时的速度,由功能关系可求得损失的机械能.
解答:解:(1)物体由静止开始向右做匀加速运动,证明电场力向右且大于摩擦力,进入磁场后做匀速直线运动,说明它所受摩擦力增大,且所受洛伦兹力方向向下.由左手定则可判断物体带负电物体带负电而所受电场力向右,说明电场方向向左.
(2)设物体被挡板弹回后做匀速直线运动的速度为v2,从离开磁场到停在C点的过程中,根据动能定理有-μmg?
=0-
m
得 v2=0.8m/s
物体在磁场中向左做匀速直线运动,其受力平衡,则有
mg=Bqv2
解得 B=0.125T≈0.13T.
(3)设从D点进入磁场时的速度为v1,据动能定理有qE?
L-μmg?
L=
m
物体从D到R做匀速直线运动,其受力平衡有
qE=μ(mg十qv1B)
解得v1=l.6 m/s,
故小物体撞击挡板损失的机械能为△E=
m
-
m
=4.8×10-4J.
(2)设物体被挡板弹回后做匀速直线运动的速度为v2,从离开磁场到停在C点的过程中,根据动能定理有-μmg?
| L |
| 4 |
| 1 |
| 2 |
| v | 2 2 |
得 v2=0.8m/s
物体在磁场中向左做匀速直线运动,其受力平衡,则有
mg=Bqv2
解得 B=0.125T≈0.13T.
(3)设从D点进入磁场时的速度为v1,据动能定理有qE?
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
物体从D到R做匀速直线运动,其受力平衡有
qE=μ(mg十qv1B)
解得v1=l.6 m/s,
故小物体撞击挡板损失的机械能为△E=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
点评:本题综合电场及磁场必质,要注意电场力做功取决于电势差而洛仑兹力不做功,故应用功能关系解决一般的运动较为简单.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011?惠州二模)利用速度传感器与计算机结合,可以自动作出物体做直线运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,由此可以知道( )
(2011?惠州二模)利用速度传感器与计算机结合,可以自动作出物体做直线运动的图象.某同学在一次实验中得到的运动小车的速度-时间图象如图所示,由此可以知道( )