Question

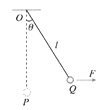
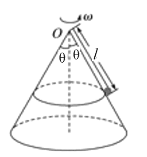
【题目】如图所示，用一根长为l＝1m的细线，一端系一质量为m＝1kg的小球(可视为质点)，另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角＝，小球在水平面 内绕锥体的轴做匀速圆周运动的角速度为rad/s，重力加速度g取10m/s2，sin＝0.6，cos＝0.8，下列法正确的是（　　）

A.这时绳的拉力大小为12.5N

B.这时绳的拉力大小约为16.7N

C.这时缓慢增大小球的角速度，绳的拉力可能不变

D.这时缓慢增大小球的角速度，绳的拉力一定变大

Answer 1

【答案】D

【解析】

AB．小球刚要离开锥面时的速度，此时支持力为零，根据牛顿第二定律得

解得

若小球的角速度，小球脱离锥体斜面，设此时α，则

联立解得

故AB错误；

CD．这时缓慢增大小球的角速度，小球离开锥面，设细线与竖直方向夹角为β，则有

得

可知这时缓慢增大小球的角速度，绳的拉力一定变大，故C错误，D正确。

故选D。