Question

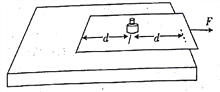
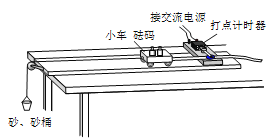
【题目】质量为M、长度为L的木板放在光滑水平地面上，在木板的左端放有一个质量为m的小木块，开始时小木块和木板都处于静止状态，某一时刻，用一水平恒力将小木块从木板左端推向右端，如图所示，若小木块与木板之间动摩擦因数为μ，且认为两者之间静摩擦力最大值与其间滑动摩擦力大小相等，小木块可视为质点．试求：若能将小木块推向木板右端，水平恒力的最小值为多大？

Answer 1

【答案】

【解析】

分别对木块m和木板M进行受力分析，根据牛顿第二定律求出各自加速度，根据木块加速度大于木板加速度求解．

小木块与木板能够产生的静摩擦力最大值为

Fmax＝μFN＝μmg

运动木板M能够产生的加速度最大值为

为使小木块能够滑向木板右端，要求小木块加速度a＞aM，即

F－Ff＝ma＞maM

F＞Ff＋maM＝μmg＋μg＝(1＋)μmg

推力最小值为F0＝(1＋)μmg.