题目内容
质量为1kg的物块从斜面底端以10m/s的速度滑上斜面，已知斜面的倾斜角为37°，物块与斜面间的动摩擦因数为0.5，已知在整个过程中，斜面都静止不动，且斜面足够长．求：
（1）从物块滑上斜面到离开斜面的过程中，物块所受各力对物块做的功及合力物块做的功；
（2）下滑过程重力做功的平均功率与回到斜面底端时重力的瞬时功率．
（1）从物块滑上斜面到离开斜面的过程中，物块所受各力对物块做的功及合力物块做的功；
（2）下滑过程重力做功的平均功率与回到斜面底端时重力的瞬时功率．
（1）在上滑过程中，由牛顿第二定律可知
mgsin37°+μmgcos37°=ma
a=gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2
上滑的位移为x=
=
m=5m
在整个过程中下降的高度为h=0
WG=mgh=0
支持力始终与位移垂直，故做功为WN=0
磨擦力做功为Wf=-2μmgxcos37°=-2×0.5×1×10×5×0.8J=-40J
合力做功为W合=WG+WN+Wf=-40J
（2）下滑过程中物体的加速度为
mgsin37°-μmgcos37°=ma
a=gsin37°+μgcos37°=10×0.6-0.5×10×0.8m/s2=2m/s2，
下滑到斜面底端时的时间为x=
at2
t=
=
s=
s
下滑到底端是速度为v=at=2
m/s
重力的平均功率为P=
=
W=6
W
重力瞬时功率为P=mgvsin37°=1×10×2
×0.6W=12
W
答：（1）从物块滑上斜面到离开斜面的过程中，重力，支持力，摩擦力做功分别为0，0，-40J及合力物块做的功为-40J；
（2）下滑过程重力做功的平均功率与回到斜面底端时重力的瞬时功率为6
W，12
．
mgsin37°+μmgcos37°=ma
a=gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2
上滑的位移为x=
| v2 |
| 2a |
| 102 |
| 2×10 |
在整个过程中下降的高度为h=0
WG=mgh=0
支持力始终与位移垂直，故做功为WN=0
磨擦力做功为Wf=-2μmgxcos37°=-2×0.5×1×10×5×0.8J=-40J
合力做功为W合=WG+WN+Wf=-40J
（2）下滑过程中物体的加速度为
mgsin37°-μmgcos37°=ma
a=gsin37°+μgcos37°=10×0.6-0.5×10×0.8m/s2=2m/s2，
下滑到斜面底端时的时间为x=
| 1 |
| 2 |
t=
|
|
| 5 |
下滑到底端是速度为v=at=2
| 5 |
重力的平均功率为P=
| mgxsin37° |
| t |
| 1×10×5×0.6 | ||
|
| 5 |
重力瞬时功率为P=mgvsin37°=1×10×2
| 5 |
| 5 |
答：（1）从物块滑上斜面到离开斜面的过程中，重力，支持力，摩擦力做功分别为0，0，-40J及合力物块做的功为-40J；
（2）下滑过程重力做功的平均功率与回到斜面底端时重力的瞬时功率为6
| 5 |
| 5 |
练习册系列答案
相关题目
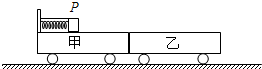处于静止状态．两车之间有一感应机关，在它的作用下，当滑块滑过两车连接处时，两车将自动分离．现剪断细线，滑块先后在甲、乙小车上滑行，最终滑块恰好滑到乙车的另一端而未滑出乙车．取g=10m/s2，求：
