Question

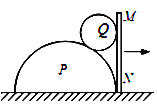
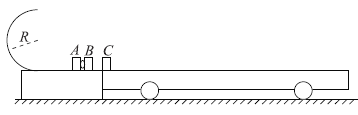
【题目】如图所示，固定的光滑平台左侧有一光滑的半圆轨道，轨道半径R=0. 72m。平台上静止着两个滑块A、B，质量分别为、，两滑块间夹有少量炸药，平台右侧有一质量M=0. 9kg的小车静止在光滑的水平面上，质量、可视为质点的滑块C静止在小车的左端，小车上表面与平台的台面等高。点燃炸药后，滑块A恰好能到达半圆轨道的最高点，滑块B冲上小车与滑块C碰后粘在一起，并且恰好没从小车右端滑出。已知滑块B、C与小车上表面间的动摩擦因数均为，g=10m/s2。

（1）求炸药爆炸后滑块B的速度大小；

（2）求滑块B、C与小车最终的共同速度的大小；

（3）求小车的长度和滑块B、C在小车上表面上的滑行时间。

Answer 1

【答案】（1）3m/s（2）0.5m/s（3）1.5m；1.5s

【解析】

（1）滑块A恰好能到达半圆轨道的最高点，则有
滑块A从半圆轨道最低点到达最高点过程中机械能守恒，由机械能守恒定律得：

mAv2+mAg2R=mAvA2

炸药爆炸过程中，炸药爆炸AB系统动量守恒，选取向右为正方向，由动量守恒定律得：-mAvA+mBvB=0

代入数据解得：vB=3m/s

（2）最终BC与小车共速，BC与小车系统动量守恒，则得：

mBvB=（mB+M +mC）v共，

解得v共=0.5m/s

（3）BC碰撞黏在一起的速度v1满足：mBvB=（mB+mC）v1

解得：v1=2m/s

BC在小车上滑行时，由能量守恒定律得：

（mB+mC）v12=（mB+mC +M）v共2+μ（mB+mC）gL

代入数据解得：L=1.5m

对小车由动量定理：μ（mB+mC）gt=M v共

解得t=1.5s