题目内容
如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,木板质量M=3kg。质量m=1kg的铁块以水平速度v0=4m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端。在上述过程中弹簧具有的最大弹性势能为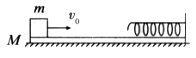
| A.3J | B.4J | C.6J | D.20J |
A
解析试题分析:设铁块与木板速度相同时,共同速度大小为v,铁块相对木板向右运动时,滑行的最大路程为L,摩擦力大小为f.根据能量守恒定律得:铁块相对于木板向右运动过程: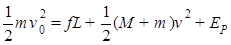
铁块相对于木板运动的整个过程: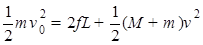 ,又根据系统动量守恒可知,mv0=(M+m)v
,又根据系统动量守恒可知,mv0=(M+m)v
联立得到:EP=3J.故选A
考点:能量守恒定律及动量守恒定律。

如图所示,在光滑的水平面上宽度为L的区域内,有一竖直向下的匀强磁场.现有一个边长为a (a<L)的正方形闭合线圈以垂直于磁场边界的初速度v0向右滑动,穿过磁场后速度减为v,那么当线圈完全处于磁场中时,其速度大小( )
A.大于 | B.等于 | C.小于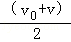 | D.以上均有可能 |
木块a和b用一根轻弹簧连接起来,放在光滑水平面上,a紧靠在墙壁上.在b上施加向左的水平力F使弹簧压缩,如图所示.当撤去外力F后,下列说法中正确的是( )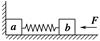
| A.a尚未离开墙壁前,a和b组成的系统动量守恒 |
| B.a尚未离开墙壁前,a和b组成的系统动量不守恒 |
| C.a离开墙壁后,a、b组成的系统动量守恒 |
| D.a离开墙壁后,a、b组成的系统动量不守恒 |
右端带有1/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )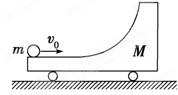
| A.小球可能从圆弧轨道上端抛出而不再回到小车 |
| B.小球不可能离开小车水平向左做平抛运动 |
| C.小球不可能离开小车做自由落体运动 |
| D.小球可能离开小车水平向右做平抛运动 |
小孩双手搭着大人的肩一起在水平冰面上以3m/s的速度向右匀速滑行,后面的小孩突然推了一下前面的大人,结果小孩以2m/s的速度向左滑行,已知小孩的质量为30kg,大人的质量为60kg,则被推后大人的速度大小变为___________。(填选项前的字母)
| A.5.5m/s | B.4.5m/s | C.3.5m/s | D.2.5m/s |
右图是“牛顿摆”装置,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高。用1、2、3、4、5分别标记5个小钢球。当把小球1向左拉起一定高度,如图甲所示,然后由静止释放,在极短时间内经过小球间的相互碰撞,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,如图乙所示。关于此实验,下列说法中正确的是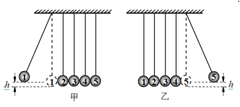
| A.上述实验过程中,5个小球组成的系统机械能守恒,动量守恒 |
| B.上述实验过程中,5个小球组成的系统机械能不守恒,动量不守恒 |
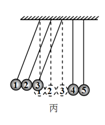
| C.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度高于小球1、2、3的释放高度 |
| D.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同 |
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ。初始时小物块停在箱子正中间,如图所示。现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,井与箱子保持相对静止。设碰撞都是弹性的,则整个过程中,系统损失的动能为 
A. | B. | C.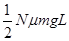 | D.(N-1)μmgL |
质量都为m的小球a、b、c以相同的速度分别与另外三个质量都为M的静止小球相碰后,a球被反向弹回,b球与被碰球粘合在一起仍沿原方向运动,c球碰后静止,则下列说法正确的是( )
| A.m一定大于M |
| B.m可能等于M |
| C.b球与质量为M的球组成的系统损失的动能最大 |
| D.c球与质量为M的球组成的系统损失的动能最大 |
