题目内容
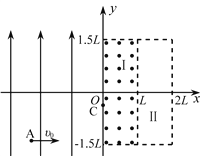
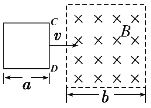
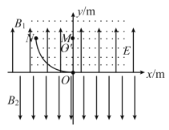
【题目】如图所示，在空间直角坐标系中，Ⅰ、Ⅱ象限（含
、
轴）有磁感应强度为
，方向垂直于纸面向外的匀强磁场和电场强度为
，方向竖直向上的匀强电场；Ⅲ、Ⅳ象限（不含轴）有磁感应强度为
，方向沿轴负方向的匀强磁场，光滑
圆弧轨道圆心
，半径为
，圆环底端位于坐标轴原点
。质量为
，带电
的小球
从处水平向右飞出，经过一段时间，正好运动到点。质量为
，带电
小球的
穿在光滑圆弧轨道上从与圆心等高处静止释放，与同时运动到点并发生完全非弹性碰撞，碰后生成小球
（碰撞过程无电荷损失）。小球、、均可视为质点，不计小球间的库仑力，取
，求：
(1)小球在处的初速度为多大；
(2)碰撞完成后瞬间，小球的速度；
(3)分析球在后续运动过程中，第一次回到轴时的坐标。
【答案】(1)
；(2)；(3)坐标位置为
【解析】
(1)
从
进入磁场，电场力和重力平衡
在洛伦兹力作用下做匀速圆周运动
洛伦兹力提供向心力
解得
(2)设
沿光滑轨道滑到
点的速度为
，由动能定理
解得
、在点发生完全非弹性碰撞，设碰后生成的
球速度为
，选向右为正方向，由动量守恒定律
解得
方向水平向右
(3)
球从轨道飞出后，受到竖直向下的电场力和垂直纸面向里的洛伦兹力，在电场力作用下，球在竖直方向做初速度为零的匀加速直线运动，在水平方向做匀速圆周运动，每隔一个周期
，
球回到
轴上，球带电量
由
及
，解得球圆周运动周期
球竖直方向加速度
球回到轴时坐标
代入数据解得
则坐标位置为
练习册系列答案
相关题目
