题目内容
(10分)宇航员站在某一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到2倍,则抛出点与落地点之间的距离为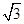 L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
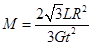
解析试题分析:设抛出点的高度为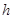 ,第一次平抛的水平射程为x则有:
,第一次平抛的水平射程为x则有: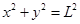 ①
①
由平抛动能的规律得知,当初速度增大到2倍,其水平射程也增大到2x,可得: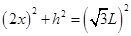 ②
②
联立解得: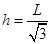 ③
③
设该星球上的重力加速度为g,由平抛运动的规律得 ④
④
由万有引力定律与牛顿第二定律得: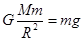 (式中m为小球的质量) ⑤
(式中m为小球的质量) ⑤
联立以上各式得: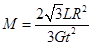
考点:平抛运动、万有引力定律

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
如图所示是一个玩具陀螺,a、b和c是陀螺上的三个点.当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是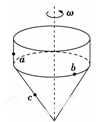
| A.a、b和c三点的线速度大小相等 |
| B.a、b和c三点的角速度相等 |
| C.a、b的角速度比c的大 |
| D.c的线速度比a、b的大 |
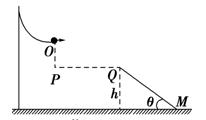
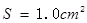 ,距离地面高度
,距离地面高度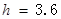 m,水从管口以不变的速度源源不断地沿水平方向射出,水落地的位置到管口的水平距离是0.9m。设管口横截面上各处水的速度都相同,空中的水的体积是多少?(
m,水从管口以不变的速度源源不断地沿水平方向射出,水落地的位置到管口的水平距离是0.9m。设管口横截面上各处水的速度都相同,空中的水的体积是多少?(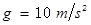 ,不计空气阻力)
,不计空气阻力)
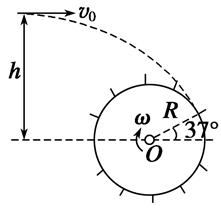
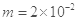 kg,电荷量q=0.2C。将弹簧保持原长拉至水平后,以初速度
kg,电荷量q=0.2C。将弹簧保持原长拉至水平后,以初速度 竖直向下射出小球P,小球P到达O点的正下方
竖直向下射出小球P,小球P到达O点的正下方 点时速度恰好水平,其大小v=15m/s。若
点时速度恰好水平,其大小v=15m/s。若 、
、 kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=lT的匀强磁场。此后,小球P在竖直平面内做半径r=0.5m的匀速圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取
kg的静止绝缘小球N相碰。碰后瞬间,小球P脱离弹簧,小球N脱离细绳,同时在空间加上竖直向上的匀强电场E和垂直于纸面的磁感应强度B=lT的匀强磁场。此后,小球P在竖直平面内做半径r=0.5m的匀速圆周运动。小球P、N均可视为质点,小球P的电荷量保持不变,不计空气阻力,取 。则。
。则。
 圆弧轨道光滑,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,到达B点时的速度为
圆弧轨道光滑,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点由静止释放,到达B点时的速度为 ,最后落在地面上C点处,不计空气阻力.
,最后落在地面上C点处,不计空气阻力.