题目内容
倾角为37°的光滑斜面上固定一个槽,劲度系数k=40N/m、原长l0=0.6m的轻弹簧下端与轻杆相连,开始时杆在槽外的长度l=0.3m,且杆可在槽内移动,杆与槽间的滑动摩擦力大小f=12N,杆与槽之间的最大静摩擦力等于滑动摩擦力.质量m=2kg的小车从距弹簧上端L=0.6m处由静止释放沿斜面向下运动,己知弹簧的弹性势能表达式Ep=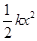 ,式中x为弹簧的形变量.g取10m/s2,sin37°=0.6,关于小车和杆运动情况,下列说法正确的是( )
,式中x为弹簧的形变量.g取10m/s2,sin37°=0.6,关于小车和杆运动情况,下列说法正确的是( )
| A.小车先做匀加速运动,后做加速度逐渐减小的变加速运动 |
| B.小车先做匀加速运动,然后做加速度逐渐减小的变加速运动,最后做匀速直线运动 |
| C.杆刚要滑动时小车已通过的位移为1.1m |
| D.杆从开始运动到完全进入槽内所用时间为0.1s |
BD
解析试题分析:对小车,刚开始受重力、斜面的支持力作用,故作加速度a=gsin37°=6m/s2的匀加速直线运动,通过L的位移后,与弹簧接触,此时的速度为:v1=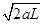 =
=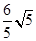 m/s,由于惯性,小车将继续沿斜面向下运动,开始压缩弹簧,在向下压缩弹簧的过程中,随着弹簧形变量的增大,其加速度将逐渐减小,由于mgsin37°=12N=f,因此当弹簧的压缩量为:x=
m/s,由于惯性,小车将继续沿斜面向下运动,开始压缩弹簧,在向下压缩弹簧的过程中,随着弹簧形变量的增大,其加速度将逐渐减小,由于mgsin37°=12N=f,因此当弹簧的压缩量为:x=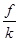 =0.3m时,杆恰好开始向槽内滑动,小车此时所受合力又恰好为零,即小车、弹簧、轻杆将整体沿斜面向下匀速运动,故选项A错误;选项B正确;当杆刚要滑动时,小车通过的位移为:s=L+x=0.9m,故选项C错误;从小车开始运动到杆刚要滑动的过程中,根据能量守恒定律有:mgssin37°=
=0.3m时,杆恰好开始向槽内滑动,小车此时所受合力又恰好为零,即小车、弹簧、轻杆将整体沿斜面向下匀速运动,故选项A错误;选项B正确;当杆刚要滑动时,小车通过的位移为:s=L+x=0.9m,故选项C错误;从小车开始运动到杆刚要滑动的过程中,根据能量守恒定律有:mgssin37°=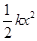 +
+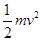 ,解得整体匀速运动的速度为:v=3m/s,从杆开始运动到完全进入槽内的过程中,整体匀速运动的位移为:l=0.3m,所用的时间为:t=
,解得整体匀速运动的速度为:v=3m/s,从杆开始运动到完全进入槽内的过程中,整体匀速运动的位移为:l=0.3m,所用的时间为:t=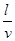 =0.1s,故选项D正确。
=0.1s,故选项D正确。
考点:本题主要考查了物体的受力分析、牛顿第二定律的瞬时性、能量守恒定律、直线运动规律的应用,以及整体法与隔离法的灵活使用、建模、分析与综合的能力问题,属于中档偏高题。

如图所示,一足够长的木板在光滑的水平面上以速度v匀速运动,现将质量为m的小物块对准木板的前端轻放,要使木板的运动速度保持不变,在物体开始接触木板到它与木板相对静止的过程中,需要对木板施加水平向右的力F,那么,在此过程中力F做功的数值为(已知物体与木板之间的动摩擦因数为μ)( )
A.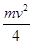 | B.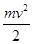 |
| C.mv2 | D.2mv2 |
一个物体从静止开始做匀加速直线运动,它在第1秒内与第2秒内位移大小之比为x1∶x2,在走完第1米时与走完第2米时的速度大小之比为v1∶v2,则下列说法正确的是:( )
| A.x1∶x2=1∶3,v1∶v2=1∶2 |
B.x1∶x2=1∶3,v1∶v2=1∶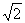 |
| C.x1∶x2=1∶4,v1∶v2=1∶2 |
D.x1∶x2=1∶4,v1∶v2=1∶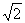 |
甲、乙两车在同一水平道路上,一前一后相距S=6m,乙车在前,甲车在后,某时刻两车同时开始运动,两车运动的过程如图所示,则下列表述正确的是( ) 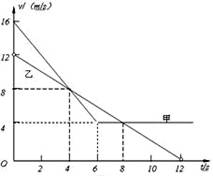
| A.当t=4s时两车相遇 |
| B.当t=4s时两车间的距离最大 |
| C.两车有两次相遇 |
| D.两车有三次相遇 |
物体由静止开始做匀加速直线运动,第7s内初速度是2.6m/s,则物体加速度是
| A.0.4m/s2 | B.0.37m/s2 |
| C.2.6m/s2 | D.0.43m/s2 |
某飞机由静止开始做匀加速直线运动,从运动开始到起飞共前进1600m,所用时间为40 s,则它的加速度a和离地时的速度v分别为( )
| A.2 m/s2 80 m/s | B.1 m/s2 40 m/s |
| C.1 m/s2 80 m/s | D.2 m/s2 40 m/s |
如图所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则xAB∶xBC等于( )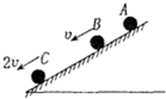
| A.1∶1 | B.1∶2 | C.1∶3 | D.1∶4 |
在平直公路上,自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们位移x(m)随时间t(s)变化规律为:汽车为x=10t- (m),自行车为x=6t(m),则下列说法正确的是( )
(m),自行车为x=6t(m),则下列说法正确的是( )
| A.汽车作减速直线运动,自行车作匀速直线运动 |
| B.不能确定汽车和自行车各作什么运动 |
| C.开始经过路标后较短时间内自行车在前,汽车在后 |
| D.当自行车追上汽车时,它们距路标96m |