题目内容
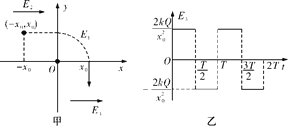
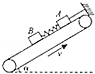
【题目】如图所示,用劲度系数k=1000N/m、原长L=10cm的轻弹簧将质量均为m=1kg的两木块A、B连在一起,放在倾角α=30°的传送带上,两木块与传送带间的动摩擦因数均为μ=![]() ,用于传送带平行的细线拉住木块A,传送带按图示方向匀速转动,两木块处于静止状态.(弹簧始终处于弹性限度内,重力加速度g=10m/s2)求:
,用于传送带平行的细线拉住木块A,传送带按图示方向匀速转动,两木块处于静止状态.(弹簧始终处于弹性限度内,重力加速度g=10m/s2)求:
(1)两木块之间的距离lAB;
(2)剪断细线瞬间,两木块加速度分别为多大.
【答案】(1)11.25cm(2)0 , 25m/s2
【解析】
对下面的木块受力分析,根据共点力平衡条件求解出弹力,根据胡克定律求解出伸长量;对下面和上面的木块分别受力分析,根据牛顿第二定律列式求解加速度。
(1)对下面的木块受力分析,受重力、支持力、平行斜面向下的滑动摩擦力、弹簧的拉力,根据平衡条件,有:mgsin30°+μmgcos30°﹣k△x=0
代入数据解得:△x=0.012m=1.25cm
故两个物体间的距离为:lAB=L+△x=10cm+1.25cm=11.25cm
(2)剪断细线瞬间,下面木块受力不变,故加速度为零;
对上面木块,受重力、支持力、弹簧的拉力、平行斜面向下的滑动摩擦力,根据牛顿第二定律,有:mgsin30°+μmgcos30°+k△x=ma
代入数据解得:a=25m/s2

练习册系列答案
相关题目