题目内容
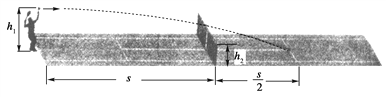
【题目】如图所示,两平行金属板A、B长8cm,两板间距离d=8cm,A板比B板电势高300V,一带正电的粒子电荷量q=10﹣10C,质量m=10﹣20kg,沿电场中心线RO垂直电场线飞入电场,初速度υ0=2×106m/s,粒子飞出平行板电场后经过界面MN、PS间的无电场区域后,进入固定在O点的点电荷Q形成的电场区域,(设界面PS右边点电荷的电场分布不受界面的影响),已知两界面MN、PS相距为12cm,D是中心线RO与界面PS的交点,O点在中心线上,距离界面PS为9cm,粒子穿过界面PS最后垂直打在放置于中心线上的荧光屏bc上.(静电力常数k=9.0×109Nm2/C2)(粒子重力忽略不计)
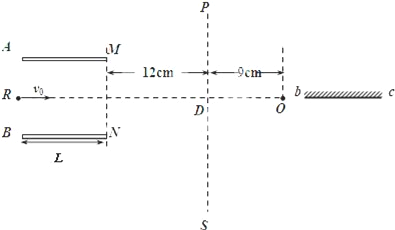
(1)求粒子穿过界面MN时偏离中心线RO的距离多远?到达PS界面时离D点多远?
(2)确定点电荷Q的电性并求其电荷量的大小.
【答案】(1)3cm 12cm (2)1.04×10﹣8C
【解析】试题分析:带电粒子垂直进入匀强电场后,做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速直线运动.由牛顿定律和运动学公式求出粒子飞出电场时的侧移量,由几何知识求解粒子穿过界面PS时偏离中心线RO的距离;由运动学公式求出粒子飞出电场时速度的大小和方向,粒子穿过界面PS后将绕电荷Q做匀速圆周运动,由库仑力提供向心力,由几何关系求出轨迹半径,再牛顿定律求解Q的电量。
(1)粒子穿过界面MN时偏离中心线RO的距离(侧向位移):
在竖直方向: ![]()
加速度为: ![]() ,
,
在水平方向: l=v0t
代入数据得:y=0.03m=3cm
带电粒子在离开电场后将做匀速直线运动,其轨迹与PS线交于a,
设a到中心线的距离为Y.
又由相似三角形得![]()
解得: Y=4y=12cm
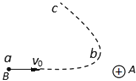
(2)带电粒子垂直进入匀强电场后,只受电场力,做类平抛运动,在MN、PS间的无电场区域做匀速直线运动,界面PS右边做圆周运动,最后垂直打在放置于中心线上的荧光屏bc上,图象如图所示:
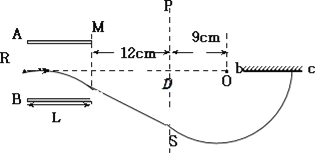
带电粒子到达a处时,带电粒子的水平速度:vx=v 0=2×106m/s
竖直速度:所以 vy=at=1.5×160m/s, v合=2.5×106m/s
该带电粒子在穿过界面PS后将绕点电荷Q作匀速圆周运动,所以Q带负电。
根据几何关系:半径r=15cm 由库仑力提供向心力: ![]()
![]()
代入数据解得:Q=1.04×10﹣8C

 期末冲刺100分创新金卷完全试卷系列答案
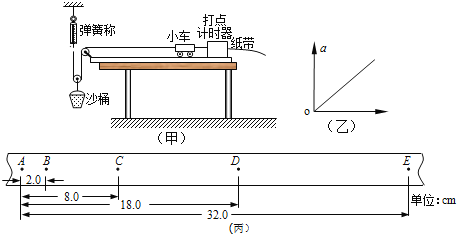
期末冲刺100分创新金卷完全试卷系列答案【题目】如图1所示为探究物体运动加速度与物体质量,物体受力关系的实验装置,砂和砂桶质量用m表示,小车和车上所加砝码总质量用M表示,小车运动加速度用a表示.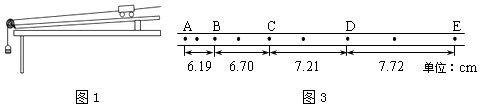
(1)实验过程中需要适当抬起长木板的一端以平衡小车所受的摩擦力,该步骤中木板被抬起的角度与小车质量(选填“有关”或“无关”)
(2)在探究加速度与小车受力关系的过程中,甲和乙两小组分别用下列两组数据进行实验操作,其中你认为合理的是(选填“甲”或“乙”)
M甲=500g M乙=500g
甲m(g) | 20 | 22 | 24 | 26 |
乙m(g) | 20 | 30 | 40 | 50 |
(3)在探究加速度与小车质量的过程中,应保持不变,通过增减小车中砝码改变小车质量M,实验测出几组a、M数据,下列图线能直观合理且正确反映a﹣M关系的是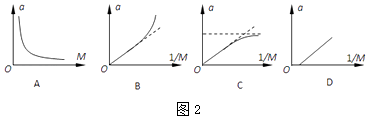
(4)图3为某次实验得到的纸带,已知实验所用电源的频率为50Hz.根据纸带可求出小车的加速度大小为m/s2 . (结果保留二位有效数字)