��Ŀ����
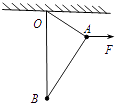
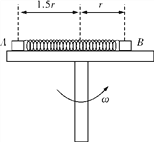
����Ŀ����ͼ��ʾ��װ��BO��O������ֱ��O��Oת��������Ϊ�ʵ��С��A����ϸ�����Ӻ�ֱ�ϵ��B��C���㣬װ�þ�ֹʱϸ��ABˮƽ��ϸ��AC����ֱ����ļнǦ�=37�㣮��֪С�������m=1kg��ϸ��AC��L=1m��B���ת���ˮƽ����;�C����ֱ������ȣ����������ٶ�gȡ10m/s2 �� sin37��=0.6��cos37��=0.8��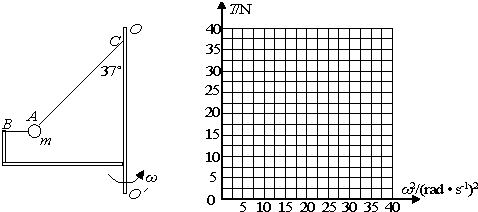
��1����װ������ת���Ľ��ٶ�Ϊ��1ʱ��ϸ��AB�ϵ�����Ϊ0��ϸ��AC����ֱ����ļн���Ϊ37�㣬����ٶȦ�1�Ĵ�С��
��2����װ������ת���Ľ��ٶ�Ϊ��2ʱ��ϸ��AB�պ���ֱ��������Ϊ0�����ʱ���ٶȦ�2�Ĵ�С��
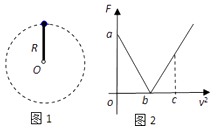
��3��װ�ÿ����Բ�ͬ�Ľ��ٶ�����ת������ͨ������������ͼ�л���ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵͼ��
���𰸡�
��1���⣺ϸ��AB������ǡΪ��ʱ��С�������������ĺ����ṩ������������ţ�ٵڶ������У�
![]()
��ã� ![]()
�𣺽��ٶȦ�1�Ĵ�СΪ ![]() rad/s
rad/s
��2���⣺ϸ��ABǡ����ֱ��������Ϊ��ʱ����ϸ��AC����ֱ����ļн�Ϊ�ȡ䣮
�ɼ��ι�ϵ�ã� ![]() ���æ�'=53��
���æ�'=53��
����ţ�ٵڶ����ɵã� ![]()
��ã� ![]()
�𣺴�ʱ���ٶȦ�2�Ĵ�СΪ ![]() rad/s
rad/s
��3���⣺�� ![]() ʱ��ϸ��ABˮƽ��ϸ��AC����������ֱ����ʼ�յ���С���������Tcos��=mg��
ʱ��ϸ��ABˮƽ��ϸ��AC����������ֱ����ʼ�յ���С���������Tcos��=mg��
��ã� ![]() ��
��
��1�ܦءܦ�2ʱϸ��AB�ɳڣ�ϸ��AC��������ˮƽ��������С����Բ���˶���Ҫ�������������У�
Tsin��=m��2lsin����T=m��2l
�أ���2ʱ��ϸ��AB����ֱ�����ֱ����Ȼ��ϸ��AC��������ˮƽ�����ṩС����Բ���˶���Ҫ����������Tsin��'=m��2lsin��'T=m��2l
���������� ![]() ʱ��T=12.5N���䣻�أ���1ʱ��T=m��2l=��2��N����T����2��ϵͼ����ͼ��ʾ
ʱ��T=12.5N���䣻�أ���1ʱ��T=m��2l=��2��N����T����2��ϵͼ����ͼ��ʾ
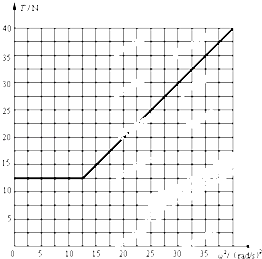
����������1��ϸ��AB������ǡΪ��ʱ��С�������������ĺ����ṩ������������ţ�ٵڶ�����������ٶȦ�1�Ĵ�С����2��ϸ��AB�պ���ֱ��������Ϊ0ʱ���ɼ��ι�ϵ���ϸ��AC����ֱ����ļнǣ�ϸ��AB�ɳڣ�����С�������������ĺ����ṩ�����������ʱ���ٶȦ�2�Ĵ�С����3������ţ�ٵڶ����ɷֱ�����ءܦ�1= ![]() rad/sʱ����1�ܦءܦ�2ʱ���أ���2ʱ�����Ĵ�С���Ӷ�ȷ��ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵ��������ͼ��
rad/sʱ����1�ܦءܦ�2ʱ���أ���2ʱ�����Ĵ�С���Ӷ�ȷ��ϸ��AC������T����ٶȵ�ƽ����2�仯�Ĺ�ϵ��������ͼ��
�����㾫����������Ҫ�����������������֪ʶ�㣬��Ҫ��������������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ��������������ȷ�����⣮

 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�