题目内容
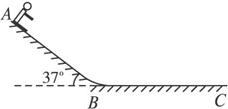
 如图(a)所示,在坐标xOy平面的第一象限内,有一个匀强磁场,磁感强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图(b)所示.规定垂直xOy平面向里的磁场方向为正,一个质量为m,电量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,在匀强磁场中运动,经过一个磁场变化周期T(未确定)的时间,粒子到达第一象限内的某一点P,且速度方向沿x轴正方向(不考虑重力作用)
如图(a)所示,在坐标xOy平面的第一象限内,有一个匀强磁场,磁感强度大小恒为B0,方向垂直于xOy平面,且随时间作周期性变化,如图(b)所示.规定垂直xOy平面向里的磁场方向为正,一个质量为m,电量为q的正粒子,在t=0时刻从坐标原点以初速度v0沿x轴正方向射入,在匀强磁场中运动,经过一个磁场变化周期T(未确定)的时间,粒子到达第一象限内的某一点P,且速度方向沿x轴正方向(不考虑重力作用)(1)若点O、P连线与x轴之间的夹角为45°,则磁场变化的周期T为多大?
(2)因点P的位置随着磁场周期的变化而变化,试求点P纵坐标的最大值为多少?此时磁场变化的周期又为多大?
分析:(1)粒子一个磁场变化周期到P点的话,其运动时间应为四分之一周期,但是要考虑顺时针和逆时针两种情况
(2)磁场变化周期越大,圆弧越长,点P的纵坐标的值越大,但在磁场变化的一个周期T'内,每个圆弧不能超过半个圆,因此圆弧最长时应是第二个圆弧与y轴相切,这样就可保证粒子不会出第一象限,求出粒子半径,可以计算P的纵坐标最大值.而磁场的变化周期T'应等于带电粒子由O点运动至P点的时间.
(2)磁场变化周期越大,圆弧越长,点P的纵坐标的值越大,但在磁场变化的一个周期T'内,每个圆弧不能超过半个圆,因此圆弧最长时应是第二个圆弧与y轴相切,这样就可保证粒子不会出第一象限,求出粒子半径,可以计算P的纵坐标最大值.而磁场的变化周期T'应等于带电粒子由O点运动至P点的时间.
解答: 解:(1)粒子仅受洛伦兹力作用而做匀速圆周运动.当磁场方向改变时,粒子的绕行方向也随之改变.要使粒子随时间T到达点P,且∠POX=45°,则粒子应正好经历
解:(1)粒子仅受洛伦兹力作用而做匀速圆周运动.当磁场方向改变时,粒子的绕行方向也随之改变.要使粒子随时间T到达点P,且∠POX=45°,则粒子应正好经历
的逆时针绕行和
的顺时针绕行(T0为粒子在磁场中作匀速圆周运动的周期).轨迹如图(a)所示.故磁场变化的周期为T=
=
(2)磁场变化周期越大,圆弧越长,点P的纵坐标的值越大,但在磁场变化的一个周期T'内,每个圆弧不能超过半个圆,因此圆弧最长时应是第二个圆弧与y轴相切(因圆弧再长就将从y轴射向第二象限穿出磁场).如图(b)所示.
设带电粒子在磁场中做圆周运动的半径为R,则
=
=R,
=2R,
=
=
R
所以点P的纵坐标为y=2R+
R=(2+
)
此时磁场的变化周期T'应等于带电粒子由O点运动至P点的时间
即 T'=
又sinθ=
=
,θ=
.ψ=
R=
解得:T'=
(1)磁场变化的周期T为
(2)点P纵坐标的最大值为
此时磁场变化的周期为
 解:(1)粒子仅受洛伦兹力作用而做匀速圆周运动.当磁场方向改变时,粒子的绕行方向也随之改变.要使粒子随时间T到达点P,且∠POX=45°,则粒子应正好经历
解:(1)粒子仅受洛伦兹力作用而做匀速圆周运动.当磁场方向改变时,粒子的绕行方向也随之改变.要使粒子随时间T到达点P,且∠POX=45°,则粒子应正好经历| T0 |
| 4 |
| T0 |
| 4 |
| T0 |
| 2 |
| πm |
| qB |
(2)磁场变化周期越大,圆弧越长,点P的纵坐标的值越大,但在磁场变化的一个周期T'内,每个圆弧不能超过半个圆,因此圆弧最长时应是第二个圆弧与y轴相切(因圆弧再长就将从y轴射向第二象限穿出磁场).如图(b)所示.
设带电粒子在磁场中做圆周运动的半径为R,则
. |
| OO1 |
. |
| O2P |
. |
| OO2 |
. |
| O1A |
| (2R)2-R2 |
| 3 |
所以点P的纵坐标为y=2R+
| 3 |
| 3 |
| mv |
| qB |
此时磁场的变化周期T'应等于带电粒子由O点运动至P点的时间
即 T'=
| 2π-2θ |
| ψ |
又sinθ=
| R |
| 2R |
| 1 |
| 2 |
| π |
| 6 |
| v |
| R |
| mv |
| qB |
解得:T'=
| 5πm |
| 3qB |
(1)磁场变化的周期T为
| πm |
| qB |
(2)点P纵坐标的最大值为
| 3R |
| 5πm |
| 3qB |
点评:本题考查带电粒子在磁场中的运动,是一道力学、电学综合题.对考生的空间想象能力及逻辑推理能力有较高的要求.求解的关键是正确想象出带电粒子的运动情景.

练习册系列答案
相关题目

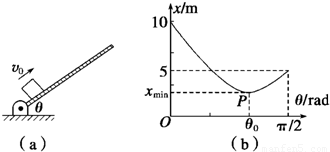
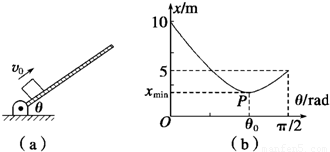
 (2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:
(2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求: