题目内容
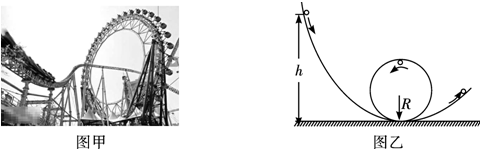
游乐场的过山车如图(a)所示,工作时,牵引机先把载人小车拉上高高的倾斜轨道顶端,然后让小车自由下滑,通过竖直圆形轨道.坐在车内的人将体验超重、失重、倒置及快速运动等感觉.现将这种情形简化成如图(b)所示模型,A点表示倾斜轨道顶端,C点和B点分别表示竖直圆形轨道的最高点和最低点,A点与B点高度差为h=30m,C点与B点高度差为d=20m,不计轨道摩擦,重力加速度g=10m/s2.求乘坐过山车时人颈椎承受的最大压力是头部重力的多少倍?


分析:人到达竖直圆形轨道的最低点B时,速度最大,颈椎受到的压力最大.先研究A到B的过程,由机械能守恒求出到达B点时的速度,再由向心力公式求解即可.
解答:解:设人的头部质量为m,颈椎承受的最大压力为Fm,人到达竖直圆形轨道的最低点B时,颈椎受到的压力最大.
设到达B点时的速度为υB,根据机械能守恒定律有:mgh=
mυB2…①;
取头部为研究对象,根据牛顿第二定律和向心加速度公式有:
Fm-mg=m
…②;
R=0.5d=10m …③
解①②③得:Fm=7mg …④
答:乘坐过山车时人颈椎承受的最大压力是头部重力的7倍.
设到达B点时的速度为υB,根据机械能守恒定律有:mgh=
| 1 |
| 2 |
取头部为研究对象,根据牛顿第二定律和向心加速度公式有:
Fm-mg=m
| ||
| R |
R=0.5d=10m …③
解①②③得:Fm=7mg …④
答:乘坐过山车时人颈椎承受的最大压力是头部重力的7倍.
点评:本题关键根据机械能守恒定律求解速度,根据牛顿第二定律求解力,是一道基础题.

练习册系列答案
相关题目
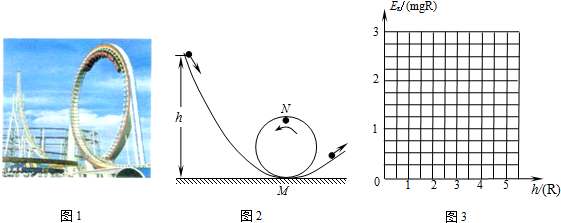
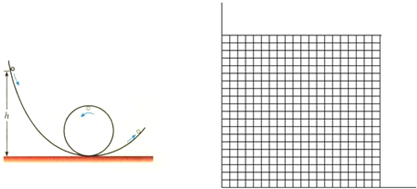
 (2006?广东)游乐场的过山车的运行过程可以抽象为如图所示的模型.弧形轨道的下端与圆轨道相接,使小球从弧形轨道上端A点静止滑下,进入圆轨道后沿圆轨道运动,最后离开.试分析A点离地面的高度h至少要多大,小球才可以顺利通过圆轨道最高点(已知圆轨道的半径为R,不考虑摩擦等阻力).
(2006?广东)游乐场的过山车的运行过程可以抽象为如图所示的模型.弧形轨道的下端与圆轨道相接,使小球从弧形轨道上端A点静止滑下,进入圆轨道后沿圆轨道运动,最后离开.试分析A点离地面的高度h至少要多大,小球才可以顺利通过圆轨道最高点(已知圆轨道的半径为R,不考虑摩擦等阻力).