题目内容
 (2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:
(2011?陕西二模)如图(a)所示,木板与水平面间的夹角θ可以在0到π/2内随意改变,可视为质点的小物块从木板的底端以大小恒定的初速率v0沿木板向上运动,所能上升的最大距离记为x,今改变θ而使x随之改变,根据所测量的若干组数据可以描绘出x-θ曲线如图(b)所示,若木板足够长,重力加速度g取10m/s2,试根据x-θ曲线和相关的物理规律,求:(1)小木块的初速率v0
(2)小木块与木板间的动摩擦系数μ
(3)对应于x-θ曲线上x取最小值的P点的坐标值(θ0,xmin)
分析:(1)由图象可知,当θ1=
时,x1=5m,此时小物块做竖直上抛运动,根据运动学公式求解小木块的初速率.
(2)由图象可知,当θ2=0时,x2=10m,当木板水平时,由动能定理得列出等式求解小木块与木板间的动摩擦系数.
(3)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理列出等式求解.
| π |
| 2 |
(2)由图象可知,当θ2=0时,x2=10m,当木板水平时,由动能定理得列出等式求解小木块与木板间的动摩擦系数.
(3)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理列出等式求解.
解答:解:(1)由图象可知,当θ1=
时,x1=5m,此时小物块做竖直上抛运动,
根据运动学公式可得:
v0=
=
m/s=10m/s
(2)由图象可知,当θ2=0时,x2=10m,当木板水平时,
由动能定理得-μmgx2=0-
m
解得μ=0.5
(3)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理得-mgxsinθ-μmgxcosθ=0-
m
解得 x=
令y=sinθ+μcosθ=
(
sinθ+
cosθ)
令 cosα=
则sinα=
所以y=
sin(α+θ)
当α+θ=
时,y存在最大值ym=
即θ0=
-α,sinθ0=cosα=
=
θ0=arcsin
对应x的最小值为xmin=
=2
m
P点坐标为(arcsin
,2
)
答:(1)小木块的初速率是10m/s,
(2)小木块与木板间的动摩擦系数是0.5.
(3)对应于x-θ曲线上x取最小值的P点的坐标值是(arcsin
,2
)
| π |
| 2 |
根据运动学公式可得:
v0=
| 2gx1 |
| 2×10×5 |
(2)由图象可知,当θ2=0时,x2=10m,当木板水平时,
由动能定理得-μmgx2=0-
| 1 |
| 2 |
| v | 2 0 |
解得μ=0.5
(3)当木板与水平方向夹角为θ时,木块沿木板上滑的距离为x,由动能定理得-mgxsinθ-μmgxcosθ=0-
| 1 |
| 2 |
| v | 2 0 |
解得 x=
| ||
| 2g(sinθ+μcosθ) |
令y=sinθ+μcosθ=
| 1+μ2 |
| 1 | ||
|
| μ | ||
|
令 cosα=
| 1 | ||
|
| μ | ||
|
所以y=
| 1+μ2 |
当α+θ=
| π |
| 2 |
| ||
| 2 |
即θ0=
| π |
| 2 |
| 1 | ||
|
2
| ||
| 5 |
θ0=arcsin
2
| ||
| 5 |
对应x的最小值为xmin=
| ||
| 2gam |
| 5 |
P点坐标为(arcsin
2
| ||
| 5 |
| 5 |
答:(1)小木块的初速率是10m/s,
(2)小木块与木板间的动摩擦系数是0.5.
(3)对应于x-θ曲线上x取最小值的P点的坐标值是(arcsin
2
| ||
| 5 |
| 5 |
点评:本题关键能够运用x-θ曲线的特殊值,选择物理规律解决问题.
了解研究对象的运动过程是解决问题的前提,选取研究过程,运用动能定理解题.
了解研究对象的运动过程是解决问题的前提,选取研究过程,运用动能定理解题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
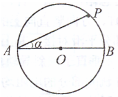 (2011?陕西二模)如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L.在以L为直径的光滑绝缘半圆环上,穿着一个带电小球+q(视为点电荷),在P点平衡.不计小球的重力,那么,PA与AB的夹角α与Q1、Q2的关系应满足( )
(2011?陕西二模)如图所示,电荷量为Q1、Q2的两个正点电荷分别置于A点和B点,两点相距L.在以L为直径的光滑绝缘半圆环上,穿着一个带电小球+q(视为点电荷),在P点平衡.不计小球的重力,那么,PA与AB的夹角α与Q1、Q2的关系应满足( ) (2011?陕西二模)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力.
(2011?陕西二模)如图所示,空间某平面内有一条折线是磁场的分界线,在折线的两侧分布着方向相反、与平面垂直的匀强磁场,磁感应强度大小都为B.折线的顶角∠A=90°,P、Q是折线上的两点,AP=AQ=L.现有一质量为m、电荷量为q的带负电微粒从P点沿PQ方向射出,不计微粒的重力. (2011?陕西二模)某同学用电压表、电流表和滑动变阻器等常规器材研究标有额定电压为3.8V字样(额定功率字迹不清)的小灯泡的伏安特性,测得的实验数据如下表所示
(2011?陕西二模)某同学用电压表、电流表和滑动变阻器等常规器材研究标有额定电压为3.8V字样(额定功率字迹不清)的小灯泡的伏安特性,测得的实验数据如下表所示