Question

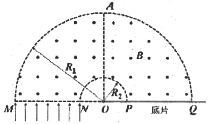
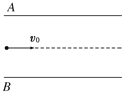
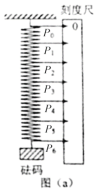
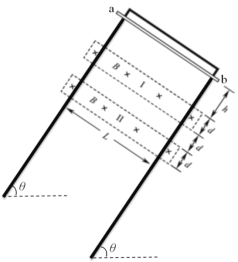
【题目】如图，倾斜固定放置的“Π”形光滑金属导轨，位于与水平面成θ角的平面内，导轨宽为L，电阻不计。宽度均为d的矩形有界匀强磁场Ⅰ、Ⅱ方向垂直导轨平面向下，磁感应强度大小均为B，两磁场间的距离也为d。质量为m、电阻为R的金属杆ab平行于导轨顶部，从距离磁场Ⅰ上边缘h处由静止释放。已知金属杆进入磁场Ⅰ和Ⅱ时的速度相等，且始终与导轨接触良好，重力加速度为g。

（1）求金属杆刚进入磁场Ⅰ时的速度v大小；

（2）定性分析金属杆穿过两磁场的过程中能量是如何变化的；

（3）分析并说明金属杆释放处与磁场Ⅰ上边缘的距离h需满足的条件；

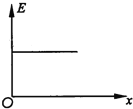
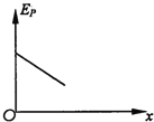
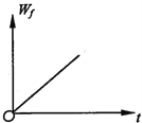
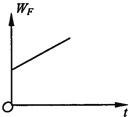
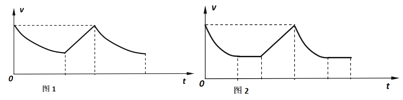
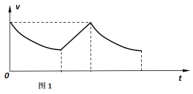
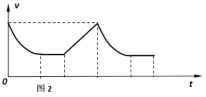
（4）作出金属杆从进入磁场Ⅰ到离开磁场Ⅱ这一过程中的v-t图像。

Answer 1

【答案】（1）；（2）金属杆穿过两磁场的过程中，重力势能减少，动能减少，机械能减少；减少的机械能转化为电路中的电能；电能再转化为内能；（3）；（4）如图所示：

【解析】

（1）金属杆进入磁场前作初速为零的匀加速直线运动，加速度

可得：

（2）金属杆穿过两磁场的过程中，重力势能减少，动能减少，机械能减少；减少的机械能转化为电路中的电能；电能再转化为内能。

（3）设杆进入磁场Ⅰ时的速度为v1,离开磁场Ⅰ时的速度为v2，进入磁场Ⅱ时的速度为v3，因为杆在两磁场区域间作匀加速直线运动，所以；

题目已知：金属杆进入磁场Ⅰ和磁场Ⅱ时的速度相等，即，可得

则杆在磁场Ⅰ内必有作减速运动的过程，所以杆刚进入磁场Ⅰ时

由以上式子可得h需满足条件：

（4）