题目内容
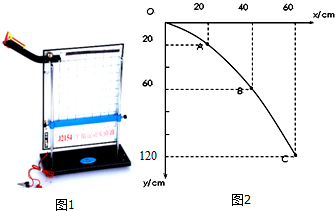
19.利用力传感器研究“加速度与合外力的关系”的实验装置如图1.
①下列关于该实验的说法,正确的是AC(选填选项前的字母)
A.做实验之前必须平衡摩擦力
B.小车的质量必须比所挂钩码的质量大得多
C.应调节定滑轮的高度使细线与木板平行
D.实验开始的时候,小车最好距离打点计时器远一点
②从实验中挑选一条点迹清晰的纸带,每5个点取一个计数点,用刻度尺测量计数点间的距离如图2所示,已知打点计时器所用电源的频率为50Hz.从图中所给的刻度尺上读出A、B两点间的距离s=0.70cm;该小车的加速度a=0.20m/s2(计算结果保留两位有效数字),实验中纸带的左(填“左”或“右”)端与小车相连接.
分析 (1)解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.注意细线的拉力是运用拉力传感器测出的,不需要满足小车的质量远大于钩码的质量.
(2)根据连续相等时间内的位移之差是一恒量求出加速度,以及A、B两点间的距离.
解答 解:①A、研究加速度与力的关系实验中,认为细线的拉力为小车的合力,所以实验前需平衡摩擦力,故A正确.
B、因为实验中用力传感器测量细线的拉力,所以不需要满足小车的质量远大于钩码的质量.故B错误.
C、细线的拉力为小车的合力,所以细线与木板平行,则应调节定滑轮的高度使细线与木板平行.故C正确.
D、实验开始的时候,小车应紧靠打点计时器,故D错误.
故选:AC.
②根据连续相等时间内的位移之差是一恒量,可知xBC-s=xCD-xBC=0.20cm,解得s=0.70cm.
根据△x=aT2得,加速度a=$\frac{△x}{{T}^{2}}=\frac{0.2×1{0}^{-2}}{0.01}m/{s}^{2}=0.20m/{s}^{2}$.
实验中纸带的左端与小车相连接.
故答案为:①AC ②0.70cm、0.20m/s2、左
点评 本题考查“加速度与合外力的关系”实验,要明确实验的原理和实验的注意事项.掌握纸带的处理方法,会通过纸带求解速度和加速度.

练习册系列答案
相关题目
7.太阳系中某行星运行的轨道半径为R0,周期为T0.但天文学家在长期观测中发现,其实际运行的轨道总是存在一些偏离,且周期性地每隔t0时间发生一次最大的偏离(行星仍然近似做匀速圆周运动).天文学家认为形成这种现象的原因可能是该行星外侧还存在着一颗未知行星.假设两行星的运行轨道在同一平面内,且绕行方向相同,则这颗未知行星运行轨道的半径R和周期T是(认为未知行星近似做匀速圆周运动)( )
| A. | T=$\frac{{{t}_{0}}^{2}}{{t}_{0}-{T}_{0}}$ | B. | T=$\frac{{t}_{0}}{{t}_{0}-{T}_{0}}$T0 | ||
| C. | R=R0$\root{3}{(\frac{{T}_{0}}{{t}_{0}-{T}_{0}})^{2}}$ | D. | R=R0$\root{3}{(\frac{{t}_{0}-{T}_{0}}{{t}_{0}})^{2}}$ |
14. 如图所示,质量为m=1kg的小球从A点水平抛出,恰好垂直撞在水平面上半圆形轨道的B点,已知h=1.6m,R=1m,θ=370,g=10m/s2,则下列说法不正确的是( )
如图所示,质量为m=1kg的小球从A点水平抛出,恰好垂直撞在水平面上半圆形轨道的B点,已知h=1.6m,R=1m,θ=370,g=10m/s2,则下列说法不正确的是( )
 如图所示,质量为m=1kg的小球从A点水平抛出,恰好垂直撞在水平面上半圆形轨道的B点,已知h=1.6m,R=1m,θ=370,g=10m/s2,则下列说法不正确的是( )
如图所示,质量为m=1kg的小球从A点水平抛出,恰好垂直撞在水平面上半圆形轨道的B点,已知h=1.6m,R=1m,θ=370,g=10m/s2,则下列说法不正确的是( )| A. | 半圆形轨道的圆心与A点的水平距离为2m | |
| B. | 小球平抛的初速度为3m/s | |
| C. | 小球到B点时重力的瞬时功率为40w | |
| D. | 若只调整A点的竖直高度,其他条件不变,则H>$\frac{196}{45}$m时,小球能够越过半圆轨道 |
4. 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
 有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )
有a、b、c、d四颗地球卫星,a还未发射,在赤道表面上随地球一起转动,b是近地轨道卫星,c是地球同步卫星,d是高空探测卫星,它们均做匀速圆周运动,各卫星排列位置如图所示,则( )| A. | a的向心加速度小于重力加速度g | B. | 在相同时间内b转过的弧长最长 | ||
| C. | c在4 h内转过的圆心角是$\frac{π}{3}$ | D. | d的运动周期有可能是20h |
11.下列说法正确的是( )
| A. | 物体的内能是物体所有分子热运动的动能和分子间的势能之和 | |
| B. | 布朗运动就是液体分子或者气体分子的热运动 | |
| C. | 气体分子间距离减小时,分子间斥力增大,引力减小 | |
| D. | 利用浅层海水和深层海水之间的温度差制造一种热机,将海水的一部分内能转化为机械能是可能的 | |
| E. | 一定量的理想气体,在压强不变时,分子每秒对器壁单位面积平均碰撞次数随着温度降低而增加 |

 如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.
如图所示,在xOy平面内,以O1(0,R)为圆心、R为半径的圆形区域内有垂直平面向里的匀强磁场B1,x轴下方有一直线ab,ab与x轴相距为d,x轴与直线ab间区域有平行于y轴的匀强电场E,在ab的下方有一平行于x轴的感光板MN,ab与MN间区域有垂直于纸平面向外的匀强磁场B2.