Question

【题目】如图所示，地日系统的两个拉格朗日点L1、L2分别位于地日之间和地球的外侧.已知地日中心距离为r，L1、L2到地球中心的距离相等均为d且与地日中心始终在一条直线上（远小于r）.两相同飞行器分别处于L1和L2点，质量均为m，与地球（质量为M）同步绕太阳（质量为M1）做圆周运动，忽略飞行器间的引力。则下列说法错误的是

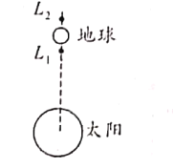
A.L1和L2向心加速度的比为（r-d）：（r+ d）

B.L1处的飞行器的线速度小于L2处的飞行器的线速度

C.太阳对两飞行器的引力之和与它对地球引力的比为M：2m

D.太阳对两飞行器的引力之和与它对地球引力的比为2m:M

Answer 1

【答案】C

【解析】

A．飞行器分别处于L1和L2点，与地球同步绕太阳做圆周运动，角速度相等，根据加速度公式可知，

则L1处飞行器和L2处飞行器向心加速度的比为

故A正确；

B．由v=r，角速度相等，半径越大，线速度越大，故B正确；

CD．对L1和L2处的飞行器，由牛顿第二定律有：

G

G

两式相加得：

太阳对地球：

G

太阳对两飞行器的引力之和与它对地球引力的比为，故C错误，D正确。