��Ŀ����
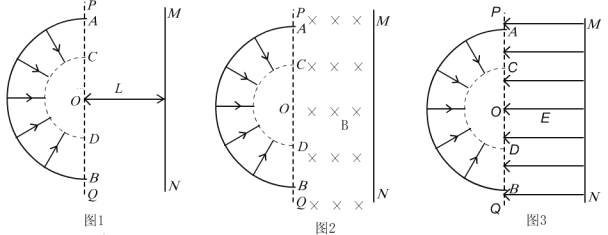
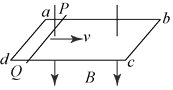
����Ŀ����ͼ��ʾ��һ���ν��������ˮƽ��ɽ��ȣ�37������L��0.4 m���ϡ������˸���һ������R0��2 ������ܵ��������ֵ��費�ƣ�����㹻������ֱ�ڽ������ƽ��ķ�����һ���ϵ���ǿ�ų����Ÿ�Ӧǿ��B��1.0 T.abΪ�����ˣ��������ýӴ���������m��0.1 kg������r��1.0 ���������ܵĶ�Ħ�������̣�0.5.���ɾ�ֹ��ʼ�»������ٶȴﵽ���Ĺ����У��϶˵���R0����������Q0��0.5 J��ȡg��10 m/s2��sin 37�㣽0.6��cos 37�㣽0.8��. ��
��1������R0����������
��2���ӿ�ʼ���ٶ����Ĺ�����ab����б���»��ľ��룻
��3����ʱ��1s��ͨ��ab��ij�������������.

���𰸡���1��I0=0.25A �� ��2��11.56 m ����3��0.5C��
��������
��1���������б���������������˶������������˶���������ﵽ����ٶ�ʱ������ƽ�⣬д������ƽ��ķ��̣������������������2��������R0�в���������Q0=0.5J�����ݽ������ɷ�����·�в����������������»������У���������ת��Ϊ���Ķ��ܡ���·�Ľ����Ⱥ�Ħ�����ȣ����ݶ��ܶ��������⣮��3��ͨ��ab�˵�������![]() ��
��
�⣺��1����������������˶�ʱ���ٶ����Ӧ�����������![]()
��ã�![]()
����R0��������Ϊ![]()
��2�������⣬��![]() ����
����![]() ��֪��·�в�����������Ϊ
��֪��·�в�����������Ϊ![]()
��Ӧ�綯��Ϊ![]()
��ʱ�˵��ٶ�Ϊ![]()
�ɶ��ܶ�������![]()
�ø��»���·����![]()
��3���������ʱ�� ʱ��1s��ͨ��ab��ij�����ĵ�������ͨ��ab�˵������� ![]()

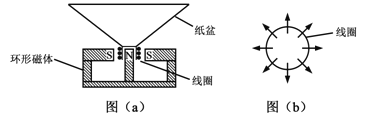
����Ŀ����УС��ͬѧ�����ij��ͭ���ߵĵ����ʣ�����������ʵ�顣
��1����ͼ����ʾ���������߷��ú��̶ȳ߲��10��ͭ������ֱ��Ϊ__________cm��

��2����ȡ����ΪL=100m��һ��ͭ���ߣ���������裬��ʵ��ǰ�������˽ͭ�ĵ����ʺ�С�����÷��������������ʱ�����ͼ�ҵ�·�����ѹ������һ��Ӧ�� _________ ![]() ����a������b��
����a������b��![]() �������õ�ѹ��ʾ��Ϊ4.50V����������ѡ��0~3.0A���̣��������ͼ����ʾ���������Ϊ________A���ɵ�ͭ�ĵ�����Ϊ _______
�������õ�ѹ��ʾ��Ϊ4.50V����������ѡ��0~3.0A���̣��������ͼ����ʾ���������Ϊ________A���ɵ�ͭ�ĵ�����Ϊ _______ ![]() (������������λ��Ч����
(������������λ��Ч����![]() ��С���ο��α��ϵ���Ϣ
��С���ο��α��ϵ���Ϣ![]() ����ͼ��ʾ
����ͼ��ʾ![]() �����ּ���õ��ĵ�������һЩƫ�����ʵ��IJ����Ѿ�ʮ�ֹ淶������ʹ�õĵ��Ҳ�Ѿ�����У��ȷ����д��һ������Ϊ�������ƫ��Ŀ���ԭ����_____��
�����ּ���õ��ĵ�������һЩƫ�����ʵ��IJ����Ѿ�ʮ�ֹ淶������ʹ�õĵ��Ҳ�Ѿ�����У��ȷ����д��һ������Ϊ�������ƫ��Ŀ���ԭ����_____��


���ֵ��������20Cʱ�ĵ����� | |||
���� | ��/ ��m | ���� | ��/ ��m |
�� | 1.6��10-8 | �� | 1.0��10-7 |
ͭ | 1.7��10-8 | ��ͭ�Ͻ� | 4.4��10-7 |
�� | 2.9��10-8 | ��ͭ�Ͻ� | 5.0��10-7 |
�� | 5.3��10-8 | �����Ͻ� | 1.0��10-6 |