题目内容
【题目】如图（a）所示，两段间距均为L的长平行金属导轨，左段表面光滑、与水平面成θ角固定放置，顶端MN之间连接定值电阻R1，右段导轨表面粗糖、水平放置，末端CD之间连接一电源，电动势为E、内阻为r，两段导轨中间EF处通过一小段绝缘光滑轨道将它们圆滑连接起来。空间存在以EF为边界的磁场，左侧为匀强磁场，方向垂直导轨平面向下，大小为B1，右侧为变化磁场，方向水平向右，大小随时间变化如图（b）所示。现将一质量为m、电阻为R2、长为L的金属棒搁在左侧顶端，由静止释放，金属棒到达EF之前已经匀速，接着进入水平轨道，且整个过程中没有离开导轨。设金属棒到达边界EF处t＝0，金属棒与水平导轨动摩擦因数为μ，重力加速度为g，则：
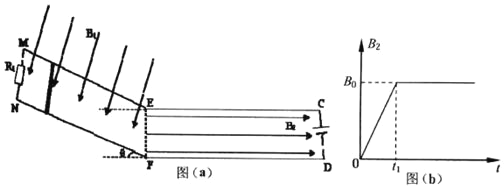
（1）金属棒到达EF处的速度大小；
（2）请写出金属棒在水平轨道运动时加速度的表达式（右侧磁感应强度用B2表示）；
（3）试通过分析，描述金属棒到达水平轨道后的运动情况。
【答案】（1）
（2）
（3）
金属棒进入水平轨道后，在
阶段：回路电流
不变, 磁场
增大, 安培力
增大，弹力
减小, 摩擦力
减小,棒作加速度逐渐减小的减速运动直至停止不动。
若金属棒
时刻速度不为零，在之后，回路电流不变，磁场保持不变，安培力不变，弹力不变，棒做匀减速运动直至停止。这种情况下，整个过程棒先做加速度减小的减速运动，接着做匀减速运动直至最后停止不动。
【解析】
（1）当金属棒在左段导轨上运动时受重力G、弹力N1、安培力FA1三个力的作用，匀速阶段受力平衡，根据平衡方程求解金属棒到达EF处的速度大小；（2）金属棒进入水平轨道，受摩擦力作用开始减速运动，分析受力情况，结合牛顿第二定律求解加速度的表达式；（3）通过分析安培力、弹力的变化情况分析加速度，从而分析物体的运动情况.
（1）当金属棒在左段导轨上运动时受重力G、弹力N1、安培力FA1三个力的作用，如图；
假设金属棒到达EF处的速度为v0，金属棒切割磁感线产生的电动势：E1=B1L1v0，
金属棒与电阻R1、导轨构成的回路的感应电流：
金属棒受到的安培力：FA1=B1I1L
因金属棒到达EF之前已经匀速，然后保持匀速运动到达EF处，匀速阶段受力平衡，则：FA1=mgsinθ
联立解得
（2）金属棒进入水平轨道的初始速度为v0，此时金属棒、导轨、电源构成闭合电路，金属棒在运动过程中受重力G、安培力FA2、弹力N2和摩擦力f四个力的作用，如图：
金属棒进入水平轨道，受摩擦力作用开始减速运动，假设减速过程中的加速度大小为a，此时回路的电流：
金属棒所受的安培力FA2=B2L2L，
摩擦力f=μN2；
由正交分解法可知：
竖直方向：N2+FA2=mg
水平方向：f=ma
联立解得
（3）①金属棒进入水平轨道后，在0-t1阶段：回路电流I2不变，磁场B2增大，安培力FA2增大，弹力N2减小，摩擦力f减小，棒做加速度减小的减速运动直至停止不动；
②金属棒t1时刻速度不为零，在t1之后，回路的电流I2不变，磁场保持不变，安培力FA2不变，弹力N2不变，棒做匀减速运动直至停止；这种情况下整个过程棒先做加速度减小的减速运动，接着做匀减速运动直至左后停止不动；具体分析讨论：
①若金属棒在0-t1阶段速度减到零，这个过程中磁场
，由 
可知金属棒运动时随着时间t的增加，加速度a逐渐减小，金属棒做加速度减小的减速运动，当金属棒的速度减为零时，磁场继续增强，安培力增大，弹力减小，因金属棒始终没有离开导轨，故其后始终保持静止状态；
②若金属棒在t1时刻的速度不为零，此后磁场保持不变，金属棒的加速度
，a不变，故此后保持匀减速直线运动，当速度为零时，安培力保持不变，弹力不变，导体棒保持静止状态；这种情况下整个过程中金属棒在0-t1阶段先做加速度减小的减速运动，t1时刻后再做匀减速直线运动，当速度为零时最后保持静止状态.
