题目内容
一长直铁芯上绕有一固定线圈M,铁芯右端与一木质圆柱密接,木质圆柱上套有一闭合金属环N,N可在木质圆柱上无摩擦移动.M连接在如右图所示的电路中,其中R为滑动变阻器, 和
和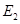 为直流电源,S为单刀双掷开关.下列情况中,可观测到N向左运动的是( )
为直流电源,S为单刀双掷开关.下列情况中,可观测到N向左运动的是( )
| A.在S断开的情况下,S向a闭合的瞬间 |
| B.在S断开的情况下,S向b闭合的瞬间 |
| C.在S已向a闭合的情况下,将R的滑动头向c端移动时 |
| D.在S已向a闭合的情况下,将R的滑动头向d端移动时 |
C
解析试题分析:由楞次定律的第二种描述:“来拒去留”可知要使N向左运动,通过N的磁通量应减小;而A、B中由断开到闭合过程中磁通量均增大,故AB错误;
若将移动滑动头,则向c端移动时,滑动变阻器接入电阻增大,则电路中电流减小,磁通量减小,故会使N左移,故C正确;
而D中向d移动时,滑动变阻器接入电阻减小时,故电路中电流增大,磁场增大,故会使N右移,故D错误;
故选C
考点:楞次定律;
点评:楞次定律有两种描述:“增反减同”和“来拒去留”,后者判断导体的运动更有效,应学会应用.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案如图所示,一粗糙的平行金属轨道平面与水平面成θ角,两轨道上端用一电阻R相连,该装置处于匀强磁场中,磁场方向垂直轨道于平面向上.质量为m的金属杆ab以初速度v0从轨道底端向上滑行,滑行到某高度h后又返回到底端.若运动过程中金属杆始终保持与导轨垂直且接触良好,轨道与金属杆的电阻均忽略不计.则下列说法正确的是( )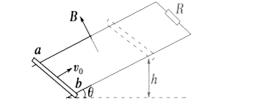
| A.金属杆ab上滑过程与下滑过程通过电阻R的电量一样多 |
B.金属杆ab上滑过程中克服重力、安培力与摩擦力所做功之和大于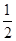 mv mv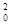 |
| C.金属杆ab上滑过程与下滑过程因摩擦而产生的内能一定相等 |
| D.金属杆ab在整个过程中损失的机械能等于装置产生的焦尔热 |
如图所示,矩形线圈abcd在匀强磁场中分别绕垂直于磁场方向的轴P1和P2以相同的角速度匀速转动,当线圈平面转到与磁场方向平行时( )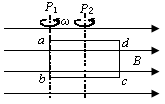
| A.线圈绕P1转动时的电流等于绕P2转动时的电流 |
| B.线圈绕P1转动时的电动势大于绕P2转动时的电动势 |
| C.线圈绕P1和P2转动时电流的方向相同,都是a→b→c→d |
| D.线圈绕P1转动时dc边的电动势大于绕P2转动时dc边的电动势 |
如图所示,导体棒ab两个端点分别搭接在两个竖直放置、电阻不计、半径相等的金属圆环上,圆环通过电刷与导线c、d相接。c、d两个端点接在匝数比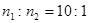 的理想变压器原线圈两端,变压器副线圈接一滑动变阻器
的理想变压器原线圈两端,变压器副线圈接一滑动变阻器 ,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动;如果变阻器的阻值为R时,通过电流表的电流为I,则( )
,匀强磁场的磁感应强度为B,方向竖直向下,导体棒ab长为L(电阻不计),绕与ab平行的水平轴(也是两圆环的中心轴)OO′以角速度ω匀速转动;如果变阻器的阻值为R时,通过电流表的电流为I,则( )
A.变阻器上消耗的功率为 |
B.ab沿环转动过程中受到的最大安培力 |
C.取ab在环的最低端时t=0,则棒ab中感应电流的表达式是 |
D.变压器原线圈两端的电压 |




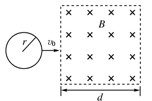
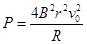


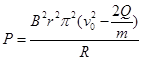

 ,质量为m,电阻为R。从某一高度竖直落入磁感应强度为B的水平匀强磁场中,磁场宽度为d,且d>l。线框
,质量为m,电阻为R。从某一高度竖直落入磁感应强度为B的水平匀强磁场中,磁场宽度为d,且d>l。线框 边刚进入磁场时线框恰好做匀速运动,此时线框的速度为__________。若线框
边刚进入磁场时线框恰好做匀速运动,此时线框的速度为__________。若线框 边刚要离开磁场时线框又恰好做匀速运动,则线框在穿过磁场的过程中产生的电能为__________。(已知重力加速度为g)
边刚要离开磁场时线框又恰好做匀速运动,则线框在穿过磁场的过程中产生的电能为__________。(已知重力加速度为g)
